Comparing Methods for Handling Missing Cost and Outcome Data in Clinical Trial-based Cost-effectiveness Analysis

Abstract

OBJECTIVES: This study compares methods for handling missing data to conduct cost-effectiveness analysis in the context of a clinical study.

METHODS: Patients in the Early Endovenous Ablation in Venous Ulceration (EVRA) trial had between 1 year and 5.5 years (median 3 years) of follow-up under early or deferred endovenous ablation. This study compares Complete-Case-Analysis (CCA), multiple imputation using linear regression (MILR) and using predictive mean matching (MIPMM), Bayesian parametric approach using the R package missingHE (BPA) and repeated measures mixed model (RMM). The outcomes were total mean costs and total mean quality-adjusted life years (QALYs) at different time horizons (1 year, 3 years and 5 years).

RESULTS: All methods found no statistically significant difference in cost at the 5% level in all time horizons, and all methods found statistically significantly greater mean QALY at year 1. By year 3, only BPA showed a statistically significant difference in QALY. Standard errors differed substantially between the methods employed.

CONCLUSION:  CCA can be biased if data are MAR, and is wasteful of the data. Hence the results for CCA are likely to be inaccurate. Other methods coincide in suggesting that early intervention is cost-effective at a threshold of £20,000 per QALY over all time horizons. However, the variation in the results across the methods does generate some additional methodological uncertainty, underlining the importance of conducting sensitivity analyses using alternative approaches.

Introduction

Missing data occurs when one or all variables are missing for a given subject. This often occurs in longitudinal studies and can particularly be a problem in within-study cost-effectiveness analysis (CEA) because accurate estimates of total mean cost and quality-adjusted life years require full data to be collected on each subject at each follow-up time point (1–3).

This study compares the results of a cost-effectiveness analysis of strategies for treating venous leg ulcers, using different methods for handling missing data. The strategies compared were early endovenous ablation of the ulcer versus delayed ablation (4). This work is unable to demonstrate which approach is “correct”, because we do not know the values of the missing data. Nevertheless, this trial provides an interesting case study because, due to the design of the trial, there was very low loss to follow-up, but considerable item missingness (see Methods: Data). The original cost-effectiveness analysis employed a repeated measure mixed model (RMM), and reported mean total cost of –£155 (95% CI, –£1262 to £953) and mean total QALY of   0.073 (95% CI, –0.06 to 0.20) at 3 years (4). RMM has been shown to have acceptable properties in simulation studies (5). However, as missing data are always unknown, it is recommended to conduct sensitivity analyses to see how robust the results are to alternative methods (1). This paper addresses this challenge using five alternative methods: complete case-analysis (CCA) (6–8), multiple imputation by linear regression (MILR), multiple imputation by predictive mean matching (MIPMM) (6,8–10), repeated measure mixed model (RMM) (11), and a Bayesian parametric approach using the R package missingHE (BPA) (12). All methods assume data are Missing at Random (MAR) (1). Results are estimated over different time horizons (and hence with different quantities of missing data) of 1, 3 and 5 years. In each case we calculate the mean incremental total cost and QALY, standard errors, the incremental cost-effectiveness ratio (ICER) and the cost-effectiveness acceptability curve (CEAC). 

Methods

Data

The Early Endovenous Ablation in Venous Ulceration (EVRA) randomised clinical trial evaluated the cost-effectiveness of early versus deferred endovenous ablation to treat venous leg ulcers. The trial methods and patients are described elsewhere (4). Briefly, resource use items in hospital, primary and community care and medications related to the treatment of venous ulceration, adverse events or complications were collected by case note review and questionnaires completed at baseline and monthly thereafter up to one year, plus one further telephone follow up between October 2018 and March 2019. 

The baseline covariates included in all the estimation models were: TREAT is treatment randomised (“early” coded as 1 or “delayed” coded as zero). The variable    is the time variable (coded as a set of categorical (dummy or factor) variables) representing the week after randomisation at which data are observed, from t=0 (baseline) to t=16 (week 260). SIZE, AGE and DURATION are the ulcer size(cm²), subject’s age (years) and length of time with ulcer (years), respectively, measured at baseline and centred at the means. SITE was coded as a factor variable. 

Each item of resource use was multiplied by UK unit costs obtained from published literature, NHS reference costs, and manufacturers’ list prices to calculate overall costs within each of these categories for each patient (4). The costs for each individual over their follow-up (from randomization to date of censoring for that individual) were assigned or apportioned into discrete time periods, that corresponded to 12 monthly periods during the first year (as follow-ups were monthly) and then yearly periods thereafter. This allowed discounting to be applied (3.5% per year), and facilitated analysis using the MI and mixed model in long format (see below).

EQ-5D-5L was collected at baseline, 6 weeks, 6 months, 12 months, plus one further telephone follow up between October 2018 and March 2019, and a utility index was calculated at each time point using a published tariff (13). 

Patients who died during the study were assigned zero costs and HRQOL thereafter. Code and example data are available in the Supplementary data, http://dx.doi.org/10.17632/j8fmdwd4jp.5.  

Missing data

Due to rigorous follow-up procedures, there were very few withdrawals or dropouts from the study. Nevertheless, data are incomplete in this study for two reasons. First, recruitment of the 450 patients into the clinical study across the 20 vascular centres took place between October 2013 and September 2016. The study finalised on March 2019. This “staggered” recruitment into the trial meant that patients had a minimum of 1 years of follow-up and a maximum of 5.5 years (median 3 years). 

Figure 1 about here (censoring pattern)

Second, all patients had regular and periodically scheduled follow-up during the first year after recruitment, but to keep the cost of the research study low, only one further telephone follow-up per patient was conducted. This took place between October 2018 and March 2019. Figure 1 shows how this study design influences the missing data pattern. A patient recruited in 2014 will have complete follow-up during the first year, missing data at years 2, 3 and 4, and one follow-up at 5 years (patient A). A patient recruited in 2015 will have complete follow-up during the first year, missing data at years 2 and 3, one follow-up at year 4, and missing data for year 5. A patient recruited in 2016 (patient C) will have complete follow-up during the first year, missing data at year 2, one follow-up at year 3, and missing data for years 4 and 5. This mainly affected collection of EQ-5D, because in the absence of telephone questionnaire data, most types of resource use and clinical outcomes could be obtained from case-notes.

The pattern of missingness was examined using descriptive statistics and via the linear logistic model (Equation 1). This can distinguish MAR from Missing Completely At Random (MAR), although cannot rule out the possibility that data are missing not at random (MNAR) (1). 

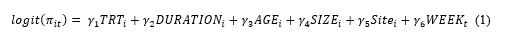
where π denotes the probability that an observation is missing in individual i at time t. 

Analytic approaches

Cost-effectiveness analysis was conducted using five analytic approaches to handle missing data: CCA, BPA, MILR, MIPMM and RMM. CCA and BPA are implemented using aggregate data, using the typology of Gabrio, A. et al. (5), while MI and RMM are implemented using disaggregated (longitudinal) data. Statistical efficiency of the MIPMM and MILR approaches were assessed by  , where FMI is the fraction of missing information and M is the number of imputed datasets. All approaches used standard statistical software (STATA or R). Further details are given in the Supplementary materials online. Table 1 summarises the approaches. 

Table 1 (summary of the approaches) about here 

Ethics and Consent

The trial was approved by the South West–Central Bristol Research Ethics Committee, and trial oversight was provided by an independent trial steering committee and an independent data and safety monitoring committee. Written informed consent was obtained from all participants. Details of the trial design and implementation are provided in the published protocol of the EVRA study (4). The study was conducted in accordance with the recommendations for physicians involved in research on human subjects adopted by the 18th World Medical Assembly, Helsinki 1964 and later revisions.

Results

Pattern of missingness

No baseline data were missing. 74% of subjects had complete data (costs and EQ-5D) at 1 year, 10% at year 3 and 25% at year 5 (Table 2). This pattern arises from the staggered recruitment and because the final questionnaire was administered at a fixed calendar point irrespective of when the subject was recruited. 

[Table 2 about here (missing data pattern)]

The logistic model showed the probability that a value is missing in costs and EQ-5D are related to the length of follow-up (week), age at baseline and site (p < 0.0001), see supplementary table S1 and table S2. From this, we assume MAR. However, it cannot be ruled out that data might be MNAR.

Only subjects with complete aggregate data were used in CCA: year 1, n=338; year 3, n=44 and year 5, n=147. The BP included all the 450 subjects. The data for RMM and MI included all the longitudinal observations for all follow-ups as an unbalanced panel.

Cost effectiveness analysis

 [Table 3 about here – results]

Table 3 shows a summary of the results of the cost-effectiveness-analysis with the five different approaches at each time point. All methods agreed that there was no statistically significant difference in cost at the 5% level at any time horizon. Early intervention was associated with statistically significantly greater mean QALY among all methods at year 1. BPA showed a statistically significant difference at year 3, while other methods tended towards greater QALY for the intervention, but this did not reach statistical significance. 

At 3 years early intervention dominated according to both RMM and BPA methods. The ICER according to CCA was £14/QALY; MI computed £489/QALY using PMM and £521/QALY using linear regression.  All methods suggested that early intervention is cost-effective at a threshold of £20,000 per QALY at 1-, 3- and 5-year time horizons. At a threshold of £20000/QALY, the estimated probability that the intervention was cost-effective was 93% using RMM and 53% using CCA, see Figure 2.

When we compare the two methods for multiple imputation, MIPMM show a loss of efficiency of 0.03% in costs using M=40 and 0.8% in QALY while MILR shows 0.20% and 1.3% for costs and QALY, respectively. MCE were less than 10% of the standard errors (SE) in both methods, indicating reasonable stability of the models. Imputations with MIPMM seemed to correspond more closely than MILR to the distribution of observed data (Supplementary Figure 1).

RMM showed greatest standard errors, SE (482) at year 1 for incremental mean costs than other methods (Figure 3a). CCA showed the greatest SE at year 3 and BPA at year 5, 769 and 807, respectively. MIPMM showed the lowest SE at all time horizons. Regarding QALY at year 1, CCA and BPA showed greater SE than other methods (Figure 3b). BPA presented the highest SE at year 3 and 5.  Other methods showed similar SE for incremental mean QALY at years 1, 3 and 5. 

[Figure 2 (ceac) and Figure 3 (SE) about here]

Discussion

This paper compared five methods for handling missing data empirically, some in common use and others less so, using a real data set with several follow-up points over a long time period.  We have attempted to use a similar estimation model in each case, so that differences arise mainly from the number of subjects and observations per subject that comprise the data, and the assumed latent correlation between observed and missing data.

The original cost-effectiveness analysis employed RMM, and reported mean total cost of –£155 (95% CI, –£1262 to £953) and mean total QALY of 0.073 (95% CI, –0.06 to 0.20) at 3 years (4) . The very small differences arise in this paper because the original paper coded SITE as a random effect. In this paper, we code SITE as a factor variable (fixed effect), because fitting the variable as a random effect for MI and BPA would have been complicated.  All the approaches coincide in estimating statistically significantly greater QALY at 1 year, but only BPA showed a statistically significant difference in QALY at 3 years. All methods suggest the mean difference in QALY is positive (in favour of early intervention). However, the mean coefficient for incremental cost is negative in some methods and positive in others, leading to differences in the ICER. 

CCA is the simplest method to implement. However, because subjects with any incomplete observations are discarded, it can be considered wasteful of the available data. Hence it is likely that the standard errors are over-estimates, arising from the low number of observations. CCA can also be biased if data are MAR. Hence the ICER for CCA is likely to be inaccurate. Other methods coincide in suggesting that early intervention is cost-effective at a threshold of £20,000 per QALY over all time horizons. However, the variation in the ICER across the methods does generate some additional methodological uncertainty, underlining the importance of conducting sensitivity analyses using alternative methods.

BPA offers a principled framework for handling missing data under the assumption of MAR. BPA includes all individuals but uses aggregate data for the dependent variables. This means that if a subject has one missing EQ-5D follow-up, then the QALY for that individual would be recorded as missing, and previous (or future) follow-ups for EQ-5D for that individual would be ignored. This means BPA can also be considered wasteful when (as is the case here) many individuals have some missing EQ-5D, in the sense that some relevant data is ignored. Hence it might be reasonable to conclude that the large standard errors generated by BPA at 3 and 5 years in this example are over-estimates. 

MI and RMM employ all the available longitudinal period cost and EQ-5D observations in all the subjects. Hence they can be considered efficient methods in the sense that no item of data is wasted. This is important when there is substantial item missingness, as we have in this dataset. Both are straightforward to implement using standard software. RMM would not be a suitable option if there were considerable missing baseline covariates (selection and CCA share this limitation). MI can impute both missing outcome data and missing baseline data. MIPMM seemed to perform somewhat better than MILR in terms of validation of imputed values against observed values in our dataset and estimated slightly lower standard errors, and greater efficiency measured by FMI/M.  Simulation studies have found that MIPMM offers a better fit to the data (14). Some caution is needed when using MIPMM if there are few donors in the vicinity of an incomplete case, leading to a risk of bias (15). Also, if a donor is selected for many individuals or repeatedly used by the same individual across imputations this will lead to inefficiency, underestimating the between-imputation variance. MI can compute the variance-covariance matrix of total mean cost and total mean QALY using parametric assumptions, while RMM estimates costs and EQ-5D separately and uses bootstrap simulations to estimate the correlation between total mean cost and total mean QALY. This makes RMM rather slow to compute, though some analysts may favour semi-parametric methods such as bootstrap when data are not normally distributed. MI is limited in the estimation commands that are available in standard software, because of the need to combine using Rubin’s rules (mi estimate in STATA). For example, fitting random effects for the sites in the estimation model might be desirable but adds extra complication. 

Standard errors for RMM were generally greater than for MIPMM in this case study. However, since we do not know the true values of the missing data, we cannot generalize about which method is “correct”. Further methodological work might conduct simulation studies comparing the two approaches under very heavy item missingness. 

Declarations

ETHICS: The trial was approved by the South West–Central Bristol Research Ethics Committee, and trial oversight was provided by an independent trial steering committee and an independent data and safety monitoring committee. The study was conducted in accordance with the recommendations for physicians involved in research on human subjects adopted by the 18th World Medical Assembly, Helsinki 1964 and later revisions.

CONSENT: Written informed consent was obtained from all participants

AVAILABILITY OF DATA AND MATERIAL: The datasets used and/or analysed during the current study are available from the corresponding author on reasonable request. Also, codes of STATA and R used in this study are available in Mendeley Data, V1, http://dx.doi.org/10.17632/j8fmdwd4jp.5. 

CONFLICTS OF INTEREST/COMPETING INTERESTS: The authors declare they have no conflicts of interest. 

FUNDING: This study was funded by the National Institute for Health Research (NIHR HTA) Programme (EVRA, project number 11/129/197). 

AUTHORS CONTRIBUTION: All authors contributed to the study conception design and analysis, and read and approved the final manuscript. 

ACKNOWLEDGEMENTS: We are grateful to the EVRA trial members for the availability of the data: Manjit S. Gohel, MD, Cambridge University Hospitals NHS Foundation Trust, United Kingdom, Jocelyn Mora, MSc, Francine Heatley, BSc, Alun H. Davies, DSc, Department of Surgery and Cancer, Imperial College London, United Kingdom; Matyas Szigeti, MSc, Jane Warwick, PhD, Imperial Clinical Trials Unit, School of Public Health, Imperial College London, United Kingdom; Andrew Bradbury, MD, University of Birmingham, United Kingdom; Richard Bulbulia, MD, Keith R. Poskitt, MD, Gloucestershire Hospitals National Health Service Foundation Trust, United Kingdom; Nicky Cullum, PhD, University of Manchester & Manchester University National Health Service Foundation Trust, United Kingdom; Isaac Nyamekye, MD, Worcestershire Acute Hospitals National Health Service Trust, United Kingdom; Sophie Renton, MS, North West London Hospitals National Health Service Trust, United Kingdom.

ADDITIONAL CONTRIBUTION: We thank the patient focus group who helped ascertain the importance of the EVRA research question, identify the most important outcome measures, and confirm the acceptability of trial interventions and follow-up protocols. As the Early Venous Reflux Ablation Trial Group, we thank the National Health Service centers and participating principal investigators and their colleagues for recruiting and monitoring trial participants: Addenbrooke’s Hospital: Manjit Gohel, MD, D. Read, P. Hayes, S. Hargreaves, K. Dhillon, M. Anwar, A. Liddle, and H. Brown; Bradford Royal Infirmary, Bradford: K. Mercer, F. Gill, A. Liu, W. Jepson, A. Wormwell, H. Rafferty, and K. Storton. Charing Cross & St Mary’s Hospitals, London: A.H. Davies, K. Dhillon, R. Kaur, E. Solomon, K. Sritharan, R. Velineni, C. S. Lim, A. Busuttil, R. Bootun, C. Bicknell, M. Jenkins, T. Lane, and E. Serjeant. Cheltenham General Hospital: K. Poskitt, R. Bulbulia, J. Waldron, G. Wolfrey, F. Slim, C. Davies, L. Emerson, M. Grasty, M. Whyman, C. Wakeley, A. Cooper, J. Clapp, N. Hogg, J. Howard, J. Dyer, S. Lyes, D. Teemul, K. Harvey, M. Pride, A. Kindon, H. Price, L. Flemming, G. Birch, H. Holmes, and J. Weston. Cumberland Infirmary: T. Joseph, R. Eiffel, T. Ojimba, T. Wilson, A. Hodgson, L. Robinson, J. Todhunter, D. Heagarty, A. Mckeane, and R. McCarthy. Derriford Hospital, Plymouth: J. Barwell, C. Northcott, A. Elstone, and C. West. Frimley Park Hospital: P. Chong, D. Gerrard, A. Croucher, S. Levy, C. Martin, and T. Craig. Hull Royal Infirmary: D. Carradice, A. Firth, E. Clarke, A. Oswald, J. Sinclair, I. Chetter, J. El-Sheikha, S. Nandhra, C. Leung, and J. Hatfield. Leeds General Infirmary: J. Scott, N. Dewhirst, J. Woods, D. Russell, R. Darwood, M. Troxler, J. Thackeray, D. Bell, D. Watson, L. Williamson, and M. Todd. Musgrove Park Hospital, Taunton: J. Coulston, P. Eyers, K. Darvall, I. Hunter, A. Stewart, A. Moss, J. Rewbury, C. Adams, L. Vickery, L. Foote, H. Durman, F. Venn, P. Hill, K. James, F. Luxton, D. Greenwell, K. Roberts, S. Mitchell, M. Tate, and H. Mills. New Cross Hospital, Wolverhampton: A. Garnham, D. McIntosh, M. Green, K. Collins, J. Rankin, P. Poulton, V. Isgar, and S. Hobbs. Northwick Park Hospital, Harrow: S. Renton, K. Dhillon, M. Trivedi, M. Kafeza, S. Parsapour, H. Moore, M. Najem, S. Connarty, H. Albon, C. Lloyd, J. Trant, and S. Chhabra. Queen Elizabeth Hospital, Birmingham: R. Vohra, J. McCormack, J. Marshall, V. Hardy, R. Rogoveanu, W. Goff, and D. Gardiner. Russells Hall Hospital, Dudley: A. Garnham, R. Gidda, S. Merotra, S. Shiralkar, A. Jayatunga, R. Pathak, A. Rehman, K. Randhawa, J. Lewis, S. Fullwood, S. Jennings, S. Cole, and M. Wall.Salisbury District Hospital: C. Ranaboldo, S. Hulin, C. Clarke, R. Fennelly, R. Cooper, R. Boyes, C. Draper, L. Harris, and D. Mead. Solihull Hospital (part of the University Hospitals Birmingham National Health System Foundation Trust): A. Bradbury, L. Kelly, G. Bate, H. Davies, M. Popplewell, M. Claridge, M. Gannon, H. Khaira, M. Scriven, T. Wilmink, D. Adam, and H. Nasr. Northern General Hospital, Sheffield: D. Dodd, S. Nawaz, J. Humphreys, M. Barnes, J. Sorrell, D. Swift, P. Phillips, H. Trender, N. Fenwick, H. Newell, and C. Mason. Royal Bournemouth General Hospital: D. Rittoo, S. Baker, R. Mitchell, S. Andrews, S. Williams, J. Stephenson, and L. Vamplew. Worcester Royal Hospital: I. Nyamekye, S. Holloway, W. Hayes, J. Day, C. Clayton, and D. Harding. York Hospital: A. Thompson, A. Gibson, Z. Murphy, T. Smith, and J. Whitwell. We thank members of our 2 oversight committees, the Trial Steering Committee (Professor Julie Brittenden [Chair]; Miss Rebecca Jane Winterborn [Consultant Vascular Surgeon]; Professor Andrea Nelson [Head of School and Professor of Wound Healing]; Dr Richard Haynes [Research Fellow and Honorary Consultant Nephrologist] and Mr Bruce Ley-Greaves [lay member] who provided invaluable input and advice as the independent lay member over the course of the study) and the Data Monitoring Committee (Professor Gerard Stansby [Chair, Professor of Vascular Surgery]; Professor Frank Smith [Professor of Vascular Surgery & Surgical Education]; Professor Marcus Flather [Professor of Medicine - Clinical Trials]; Dr Ian Nunney [Medical Statistician]) for their support and guidance. There was no financial compensation for these contributions.

References

1.          Faria R, Gomes M, Epstein D, White IR. A Guide to Handling Missing Data in Cost-Effectiveness Analysis Conducted Within Randomised Controlled Trials. PharmacoEconomics [Internet]. 2014 Dec 29;32(12):1157–70. Available from: http://link.springer.com/10.1007/s40273-014-0193-3

2.          Myers WR. Handling Missing Data in Clinical Trials: An Overview. Therapeutic Innovation & Regulatory Science. 2000;34(2):525–33. 

3.          Fitzmaurice G, Laird N, Ware J. Applied longitudinal Analysis (2nd Edition). Wiley. 2011;http://biosun1.harvard.edu/~fitzmaur/ala/. 

4.          Gohel MS, Mora, MSc J, Szigeti M, Epstein DM, Heatley F, Bradbury A, et al. Long-term Clinical and Cost-effectiveness of Early Endovenous Ablation in Venous Ulceration. JAMA Surgery [Internet]. 2020 Dec 1;155(12):1113. Available from: https://jamanetwork.com/journals/jamasurgery/fullarticle/2770717

5.          Gabrio A, Hunter R, Mason AJ, Baio G. Joint Longitudinal Models for Dealing With Missing at Random Data in Trial-Based Economic Evaluations. Value in Health [Internet]. 2021;24(5):699–706. Available from: https://doi.org/10.1016/j.jval.2020.11.018

6.          Leurent B, Gomes M, Carpenter JR. Missing data in trial-based cost-effectiveness analysis: An incomplete journey. Health Economics (United Kingdom). 2018;27(6):1024–40. 

7.          Carroll OU, Morris TP, Keogh RH. How are missing data in covariates handled in observational time-to-event studies in oncology? A systematic review. BMC Medical Research Methodology. 2020;20(1):1–15. 

8.          Manca A, Palmer S. Handling missing data in patient-level cost-effectiveness analysis alongside randomised clinical trials. Applied Health Economics and Health Policy. 2005;4(2):65–75. 

9.          Hayati Rezvan P, Lee KJ, Simpson JA. The rise of multiple imputation: A review of the reporting and implementation of the method in medical research Data collection, quality, and reporting. BMC Medical Research Methodology. 2015;15(1):1–14. 

10.        White IR, Royston P, Wood AM. Multiple imputation using chained equations: Issues and guidance for practice. Statistics in Medicine. 2011;30(4):377–99. 

11.        Cox E, Saramago P, Kelly J, Porta N, Hall E, Tan WS, et al. Effects of Bladder Cancer on UK Healthcare Costs and Patient Health-Related Quality of Life: Evidence From the BOXIT Trial. Clinical Genitourinary Cancer [Internet]. 2020;18(4):e418–42. Available from: https://doi.org/10.1016/j.clgc.2019.12.004

12.        Ma Z, Chen G. Bayesian methods for dealing with missing data problems. Journal of the Korean Statistical Society. 2018;47(3):297–313. 

13.        van Hout B, Janssen MF, Feng YS, Kohlmann T, Busschbach J, Golicki D, et al. Interim scoring for the EQ-5D-5L: Mapping the EQ-5D-5L to EQ-5D-3L value sets. Value in Health [Internet]. 2012;15(5):708–15. Available from: http://dx.doi.org/10.1016/j.jval.2012.02.008

14.        Marshall A, Altman DG, Royston P, Holder RL. Comparison of techniques for handling missing covariate data within prognostic modelling studies: A simulation study. BMC Medical Research Methodology. 2010;10. 

15.          Morris TP, White IR, Royston P. Tuning multiple imputation by predictive mean matching and local residual draws. BMC Medical Research Methodology. 2014;14(1).

Tables

Table 1. Overview of approaches employed to handle missing data.

† If aggregate data are used, there will be one observation per patient.  If longitudinal data are used, the inputs to the model may consist of several observations per patient. 

Table 2. Missing data pattern.

Table 3. Results of the models.

Note: RMM. repeated measure mixed model; CCA. complete-case-analysis; MIPMM. Multiple Imputation using predictive mean matching; MILR. Multiple Imputation using linear regression; BPA. Bayesian parametric approach; QALY. quality-adjusted life years; ICER. incremental cost ratio.