Overview
A forest plot is a graphical representation of a meta-analysis that visualizes the association of all studies included in the meta-analysis in relation to each other and demonstrates the pooled effect estimate and heterogeneity of all results. Forest plots were developed in the 1980s, but the name was coined in 1996 because these plots look like a “forest of lines.”
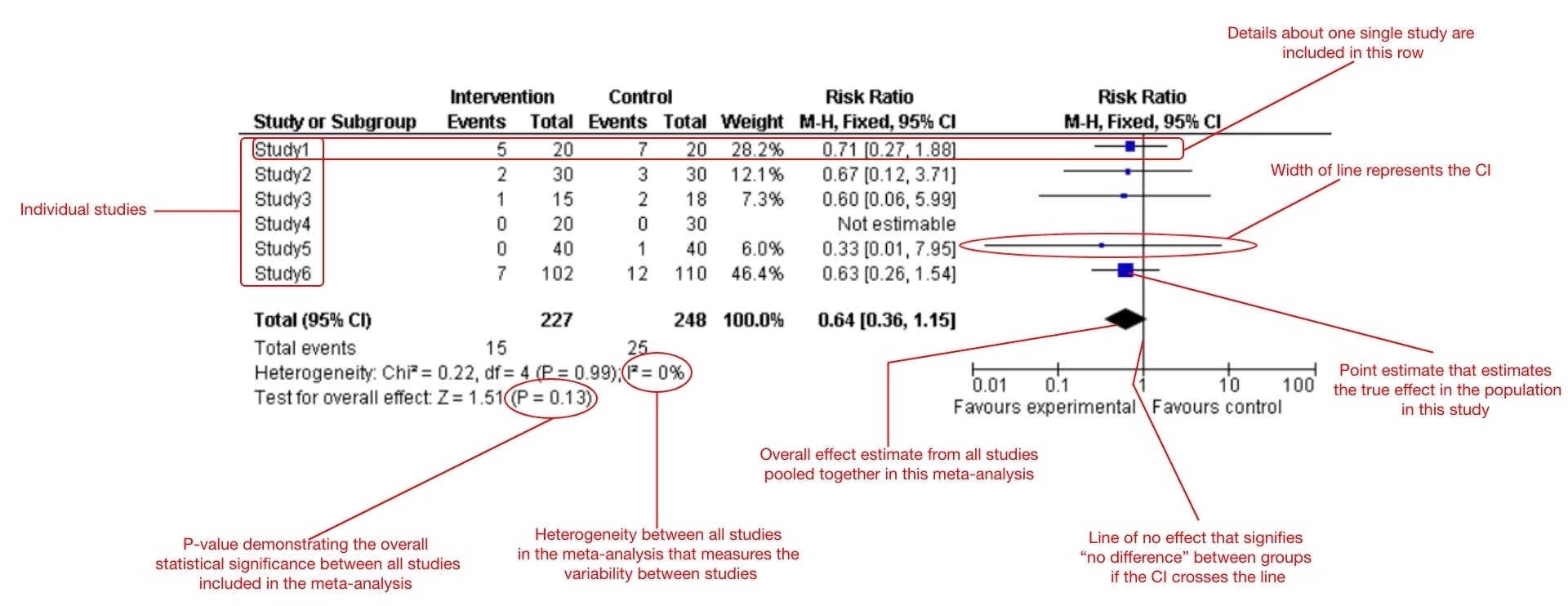
The parts of a Forest Plot
- Each study is represented by a horizontal line. The number of events, the effect estimate, and the 95% confidence intervals of each study are shown. If no events occurred in the study, then no line is displayed in the plot.
- The width of the line represents the range of the confidence interval: the range within which one can be 95% confident that the true value lies.
- The box on each study’s line represents the point estimate of that study, which is the best guess of the true effect in that population. The size of the box represents the “weight” of the study. The weight of the study depends on the statistical model used to combine the studies in the meta-analysis, the number of events, and the overall number of participants in the trial. The larger the study, the larger the box. Boxes are visualized in this manner to draw the eyes toward the studies that have more weight.
- The diamond represents the pooled effect estimates and confidence intervals from all studies included in the meta-analysis.
- The line down the middle represents the line of no effect. If a study’s line crosses the line of no effect, there is no statistical difference between groups in this study. Similarly, if the diamond crosses the line of no effect, there is no statistical difference between groups amongst all trials in the meta-analysis. Conversely, if a study’s line or the diamond does not cross the line of no effect, a statistically significant difference is demonstrated within the trial and amongst all trials, respectively.
- When the outcome is a negative outcome (mortality, heart attacks, pain, etc.) the intervention is displayed on the left side of the forest plot and the comparator (control) on the right side. If the point estimates land on the left side of the line of no effect and the confidence interval and diamond do not cross the line, the intervention successfully reduces the negative event (lower mortality, less heart attacks, reduced pain). The converse direction is true for good outcomes, such as health-related quality of life, satisfaction, happiness, etc. If the point estimates land on the right side of the line of no effect and the confidence interval and diamond do not cross the line, the intervention improves the positive outcome.
- Statistics such as the heterogeneity (I-squared), overall effect size, and P-value are shown alongside a forest plot. Heterogeneity conveys if all studies in the meta-analysis measured the same thing and measures the variability between studies, or in other words, how different the trials are from each other. Heterogeneity can be due to differences in methodologies, statistics, effect sizes, or clinical parameters between participants. The greater the percentage of heterogeneity, the less the results can be trusted. Generally, 30% or less is considered mild heterogeneity and the results are more likely to be valid, while 70% or more indicates significant heterogeneity, which leads to questionable results. Over 70% heterogeneity means the researchers should consider not meta-analyzing the results because high heterogeneity may indicate that the effect demonstrated in the meta-analysis is not valid.
Figure 1: The parts of a forest plot.
Advantages
Forest plots visually demonstrate the overall relationship studies have to each other in an meta-analysis and illustrate the consistency, precision, and heterogeneity of studies' individual results and the collective results of all trials included in a meta-analysis.
Caveats
- The validity of the meta-analysis results depend on the quality, precision, and accuracy of the results from the individual trials that are included in the meta-analysis. If the original study-level data is biased, the meta-analysis results will also be biased. A properly conducted systematic review that includes a meta-analysis will evaluate the bias and provide conclusions placing the results of the meta-analysis in context to the risk of bias of the included trials.
- The results computed in a meta-analysis and depicted in a forest plot depend on the model used to meta-analyze results. There are two primary models: 1) the fixed effect meta-analysis; and 2) the random effect meta-analysis. Briefly, the fixed effect model assumes all studies in the meta-analysis estimate the same quantity. This is analogous to tossing a coin the same number of times in multiple experiments and observing the number of heads and tails in each experiment. If there is a low amount of heterogeneity, the fixed effect model can be used. Conversely, if there is a moderate or high level of heterogeneity, the random effect model is more appropriate since it assumes there is more variability within each experiment and is the more conservative model. In general, it is better if conservative results have been presented, since many trials are conducted with different methodologies and diverse patients. Hence, the random effect model is the most appropriate option for many meta-analyses.
What to Watch For
- Where the studies fall in relation to the line of no effect and whether the studies consistently fall on the same or the opposite side of the line is important. If the studies fall on the same side, this demonstrates consistency between studies. If the confidence intervals do not overlap, there is heterogeneity regardless of whether the studies are all (or mostly) on the same side of the line of no effect (Figure 2).
- The larger the confidence intervals of the trial, the lower the precision and the greater the uncertainty. Similarly, the greater the width of the overall pooled effect size, the greater the uncertainty.
- If the lines of the confidence intervals do not overlap by at least 1/3, it suggests there may be inconsistency. If the confidence intervals do overlap there is no - or at least less - heterogeneity. If the point estimates are scattered on different sides of the line of no effect but the confidence intervals have good overlap, this also suggests no or low heterogeneity.
- The larger the effect size and the smaller the p-value, the more pronounced the effect and the greater the statistical significance.
- The higher the I-squared value, the greater the heterogeneity. If the p-value is significant and the heterogeneity is high, the heterogeneity is statistically significant.
Figure 2: Assessing heterogeneity in a forest plot

Also Read:
Explainer: What is a Systematic Review and Meta-analysis?
How the Dissemination Crisis Led to the Replication Crisis
![[object Object]](https://images.prismic.io/researchsquare/dbdc098d-3122-46ec-a8eb-9094a77dc237_RS+Blog-Explainer-Forest+Plots.png?auto=compress,format&rect=0,0,600,400&w=600&h=400)