Evaluation of Earth System Model and Atmospheric Inversion using Total Column CO2 Observations from GOSAT and OCO-2

doi:10.21203/rs.3.rs-53348/v2

Download PDF

Research article

Evaluation of Earth System Model and Atmospheric Inversion using Total Column CO₂ Observations from GOSAT and OCO-2

https://doi.org/10.21203/rs.3.rs-53348/v2

This work is licensed under a CC BY 4.0 License

Journal Publication

published 14 Apr, 2021

Read the published version in Progress in Earth and Planetary Science →

You are reading this older preprint version

Read the latest preprint version →

The measurements of one of the major greenhouse gases, carbon dioxide (CO₂), are being made using dedicated satellite remote sensing since the launch of the greenhouse gases observing satellite (GOSAT) by Japan Aerospace Exploration Agency (JAXA) in 2009 and National Aeronautics and Space Administration (NASA) Orbiting Carbon Observatory-2 (OCO-2). In the past 10 years, estimation of CO₂ fluxes from land and ocean using the earth system models (ESMs) and inverse modelling of in situ atmospheric CO₂ data have also made significant progress. In this article, we attempt, for the first time, to evaluate the CO₂ fluxes simulated by an earth system model (MIROC-ES2L) using GOSAT observations and the fluxes estimated by an inverse model (MIROC4-Inv) for the period 2009-2014. Further, we use the OCO-2 measurements for testing the consistency of inversion results for the period 2014-2018, along with the GOSAT data. Both MIROC-ES2L and MIROC4-Inv fluxes are used in the MIROC4-atmospheric chemistry transport model (referred to as ACTM_ES2LF and ACTM_InvF, respectively) for calculating CO₂ concentrations that are sampled at the time and location of the satellite measurements. Our results suggest the inverse model using in situ data are more consistent with the OCO-2 retrievals, compared to those of the GOSAT XCO₂ data, suggesting possible improvements in the present GOSAT retrieval system by better accounting for the degradation correction of the Thermal And Near infrared Sensor for carbon Observations - Fourier Transform Spectrometer (TANSO-FTS). The ACTM_ES2LF simulation shows a slightly weaker seasonal cycle for the meridional profiles of CO₂ fluxes, compared to that from the ACTM_InvF. This difference is revealed by greater XCO₂ differences for ACTM_ES2LF vs GOSAT, compared to those of ACTM_InvF vs GOSAT. Using remote sensing based global products of leaf area index (LAI) and gross primary productivity (GPP) over land, we show a weaker sensitivity of MIROC-ES2L biospheric activities to the weather and climate in the tropical regions. Our results clearly suggest the usefulness of XCO₂ measurements by satellite remote sensing for evaluation of large-scale ESMs, which so far remained untested by the sparse in situ data.

Environmental Engineering

Carbon dioxide (CO2)

Global and regional carbon cycle

Earth System Model

Inverse model

Atmospheric Chemistry-Transport Model

Carbon dioxide (CO₂) is the most important anthropogenically produced greenhouse gas (Fosters et al., 2013). During 2009-2018, CO₂ emissions associated with human activities, such as the burning of fossil fuel and cement manufacturing contributed about 100 PgC (1 Pg=10¹⁵ g) or about 10 PgC/yr to the atmosphere (Friedlingstein et al. 2019). Based on available statistics (Janssens-Maenhout et al. 2019), about 60% of these emissions originate from the northern extratropics, mainly by the Annex 1 countries of the UN Framework Convention on Climate Change (UNFCCC), signatories to the Kyoto Protocol subject to caps on greenhouse gases (GHGs) emissions. The inventory emissions from the non-Annex I countries are rising quickly due to their rapid economic growth and shifting manufacturing from the Annex I or Organisation for Economic Co-operation and Development (OECD) member countries to the so-called BRICS countries (i.e. Brazil, Russia, India, China, and South Africa). Uncertainties in the emissions are larger for non-Annex I counties relative to the Annex I countries (Andres et al. 2012). This leads to lower confidence of our knowledge of the changes in terrestrial biospheric fluxes in response to climate change and climate variabilities, and CO₂ fertilisation feedbacks (Saeki and Patra 2017; Bastos et al. 2020).

CO₂ emissions to the atmosphere from land use change (LUC), predominantly caused by human driven deforestation and cropland development, is estimated to be in the range of 1-2 PgC/yr for the period 2009-2018 (Hansis et al. 2015; Houghton and Nassikas 2017; Friedlingstein et al. 2019). The uncertainties in LUC CO₂ emission estimations are originated from treatment of various terrestrial carbon pools of above and below ground biomass and soil carbon (Houghton and Nassikas 2017; Friedlingstein et al. 2019; Kondo et al. 2020). Due to an increase in these anthropogenic emissions, the atmospheric CO₂ concentration is rising at an average rate of 3 ppm/yr during 2009-2018 (Tans and Keeling 2019). This is less than half of a rate that is expected from all anthropogenic emissions. About 29% of the anthropogenic emissions are taken up by the land ecosystems due to greater availability of CO₂ in the atmosphere thereby increasing water use efficiency by the plants (Keeling et al. 2017). About 23% is being absorbed by the oceans as the partial pressure of CO₂ increases faster in the atmosphere than in the surface ocean (DeVries et al. 2019).

In the Paris Agreement (2015), parties to the UNFCCC reached a landmark agreement to combat climate change and to accelerate and intensify efforts to reduce the rate of atmospheric CO₂ build-up to limit increase of the Earth’s global-mean surface air temperature to below 2^oC by 2100. Meeting this goal will depend very strongly on the land-ocean-atmosphere feedbacks in the future (Ciais et al. 2013). One of the urgent questions is whether or not the terrestrial biosphere and the oceanic systems will continue to absorb and store CO₂ from atmosphere in future, particularly when the emission mitigation goals of net-zero or negative emissions are achieved in the later-half of the century (Jones et al. 2019). For this purpose, comprehensive Earth System Models (ESMs) have been developed that account for the past behaviours of the terrestrial and oceanic climate systems, coupled with the carbon and nutrients cycles (Jones et al. 2016; Arora et al. 2019; Hajima et al. 2020). The ESM simulated land/ocean-atmosphere CO₂ fluxes are relatively untested in comparison with the atmospheric constraints, while the CO₂ fluxes simulated by the dynamic global vegetation models (DGVMs) are recently benchmarked with the global remote sensing CO₂ data products or climate parameters (Calle et al., 2019; Collier et al., 2018).

The main goal of this study is thus to evaluate the CO₂ fluxes simulated using one such ESMs, the JAMSTEC’s Model for Interdisciplinary Research on Climate (MIROC)-based Earth System Simulation version 2 (referred to as MIROC-ES2L) (Hajima et al. 2020). As the in situ measurements are often affected by local weather conditions and spatial coverage is sparse, the global ESM simulations of CO₂ will not be adequately assessed by comparing with in situ data. With the advent of satellite remote sensing by the dedicated instruments for CO₂ measurements, we now have global coverage of CO₂ concentrations since 2009 (Yoshida et al. 2013). This has allowed us to attempt for the first time, to the best of our knowledge and to check performance of ESM simulations for the recent five years (2009-2014) using the historical CMIP6 simulations, which are only conducted up to 2014 as per the protocol. We also compare the MIROC-ES2L simulation results with an inversion estimation of CO₂ fluxes using in situ CO₂ measurements (Saeki and Patra 2017; Friedlingstein et al. 2019).

The details of the materials and method for MIROC-ES2L evaluation are given in Section 2, followed by the results and discussion in Section 3. Conclusions are given in Section 4.

Greenhouse gases Observing SATelite, retrieval version 02.81 (GOSAT_v2.81)

Orbiting Carbon Observatory, retrieval version 9r (OCO2_v9r)

The Orbiting Carbon Observatory - 2 (OCO-2) was launched on 04 July 2014 and retrievals are available since September 2014 (Crisp et al. 2017; Eldering et al. 2017). We have used bias-corrected retrievals, version 9r (OCO-2_v9r) (Updated Lite files from https://co2.jpl.nasa.gov/#mission=OCO-2) (O’Dell et al. 2018). OCO-2 data are available for XCO₂, a priori profiles (20 levels) and column averaging kernels (20 pressure levels). Data with quality flag of 0 (best data) are used in the analysis. The data coverage of OCO-2 (approximately 10 million data points annually) is much greater than that of GOSAT (approximately 0.1 million data points annually). The single-shot accuracy of OCO-2 retrievals is estimated to be 1.3 ppm over land and 1 ppm over ocean (Kulawik et al., 2020). The better quality of the XCO₂ data from OCO-2 (compared to bias uncorrected GOSAT_v2.81), although without an overlap with the MIROC-ES2L simulation, provides us an assessment of the retrieval data quality on evaluation of the CO₂ flux models.

MIROC Earth System model version 2 for Long-term simulations (MIROC-ES2L) and evaluation using remote sensing observations

MIROC-ES2L is the latest generation of earth system model (ESM) that is developed at the JAMSTEC, in collaboration with Tokyo University and the National Institute for Environment Studies (NIES). The ESM has fully coupled terrestrial-ocean-atmosphere model components for simulating the evolutions of carbon-nitrogen cycles and climate for the past centuries and centuries to millennium-term future projection (Hajima et al., 2020),. The horizontal resolution of the atmosphere is T42 spectral truncation (approximately 2.8◦ intervals for latitude and longitude) and the vertical resolution is 40 layers up to 3 hPa with a hybrid σ –p coordinate; the ocean grid system consists of horizontally 360 × 256 grids with 62 vertical layers.

The terrestrial carbon cycle component covers major processes relevant to global carbon cycle, with vegetation (leaf, stem, and root), litter (leaf, stem, and root), and humus (active, intermediate, and passive) pools and with a static biome distribution. Photosynthesis or gross primary productivity (GPP) is simulated based on the Monsi–Saeki theory (Monsi and Saeki 1953), and the allocation of photosynthate between carbon pools in vegetation (e.g., leaf, stem, and root) is regulated dynamically following phenological stages. The transfer of vegetation carbon into litter–soil pools is simulated using constant turnover rates, and in deciduous forests, seasonal leaf shedding occurs at the end of the growing period. The perturbation from land-use change on terrestrial carbon cycle is simulated by the transition of 5 types of land-use tiles (primary vegetation, secondary vegetation, urban, crop, and pasture) in a grid; e.g., deforestation processes are represented by the reduction in area fraction of primary/secondary vegetation (and increase of less-vegetated land-use tile like urban), and deforested carbon is gradually lost to the atmosphere. Details on carbon cycle processes in the model can be found elsewhere (Ito and Oikawa 2002; Hajima et al. 2020).

In the Ocean ecosystem component Embedded within the ocean circulation model (OECO2), ocean biogeochemical dynamics are simulated with 13 biogeochemical tracers (three types of nutrients, four biological tracers, four carbon and/or calcium, and other two inorganic tracers). The carbon cycle processes are simulated following the biogeochemical dynamics of the tracers, assuming that all organic materials have identical elemental stoichiometric ratio. Ocean ecosystem dynamics are simulated based on the nutrient cycles of nitrate, phosphorous, and iron. The nutrient concentration, in conjunction with the controls of seawater temperature and the availability of light, regulates the primary productivity of the phytoplankton. In the model, zooplankton is assumed to be independent of abiotic conditions (e.g., seawater temperature) and dependent on biotic conditions (phytoplankton and zooplankton concentrations). Detritus contains nitrate, phosphorus, iron, and carbon, most of which is remineralized while sinking downward. A fraction of the detritus that reaches the ocean floor is removed from the system. The formulations of atmosphere–ocean gas exchange, carbon chemistry, and related parameters follow protocols from the Ocean Model Intercomparison Project (OMIP) (Orr et al. 2017).

The basic performance of the land and ocean carbon cycle are assessed by comparing the simulated spatial patterns with observation data for land (gross primary production, vegetation carbon and soil carbon for the land component) and ocean (primary production, export production, atmosphere-ocean CO₂ flux, dissolved inorganic carbon) (Hajima et al. 2020). Hajima et al. (2020) also showed that atmosphere-land or ocean CO₂ fluxes in cumulative value (i.e., the changes in land or ocean amount) in the period of 1850-2014 are within the estimated range suggested by Le Quéré et al. (2018), although the GPP seasonality in land tropics and CO₂ flux seasonality in the Southern Ocean and the North Atlantic Ocean requires improvement. The feedback strengths of carbon cycle processes, which is associated with the magnitude of natural carbon sinks in response to atmospheric CO₂ concentration and climate change, are also quantified and compared with other ESMs, showing MIROC-ES2L has the intermediate values for the feedback parameters (Arora et al. 2020).

The original historical simulation of MIROC-ES2L is obtained from the CMIP6 exercise (Eyring et al. 2016; Hajima et al. 2020), where the model is driven by anthropogenic fossil fuel CO₂ emission, other GHGs and aerosol emissions/concentrations, natural forcing like solar irradiance change and volcanic events, and land-use change. The CO₂ concentration is explicitly simulated by the model based on the external forcing of anthropogenic CO₂ emission, simulated land and ocean CO₂ sink, and simulated LUC-derived CO₂ emission (the experimental configuration in which CO₂ concentration is prognostically simulated by models is called "emission-driven" mode, while the configuration in which CO₂ concentration is prescribed as forcing data is called “concentration-driven” mode) (Jones et al., 2016). The simulation period was 1850-2014, following a continuous 2483 spin-up years by the “concentration-driven” mode and 691 years by the “emission-driven” mode. The accuracy of future prediction by the ESMs is likely to depend on the quality of the historical simulation of the carbon-nitrogen-climate feedbacks and the model response to external forcing (e.g., terrestrial response to land-change forcing). However, the sparse in situ measurements and smaller flux footprint of the surface sites limited the evaluation of the historical simulations by the ESMs. The situation has now changed because of the global coverage of XCO₂ measurements from space (GOSAT and OCO-2), which are explored in this study for an evaluation of the MIROC-ES2L historical simulation.

MIROC Atmospheric Chemistry-Transport model (MIROC4-ACTM)

The MIROC (version 4) – based atmospheric chemistry transport model (MIROC4-ACTM) simulations are conducted at horizontal resolution of T42 spectral truncations with 67 hybrid pressure layers in vertical. The greater number of vertical layers covering the altitude range from Earth’s surface to 0.0128 hPa or about 80 km, and closely spaced levels in the upper troposphere and lower stratosphere region is designed for better representation of the vertical profiles of long-lived gases in the Earth’s atmosphere. MIROC4-ACTM (Patra et al., 2018; Watanabe et al., 2011) simulated horizontal winds and temperature are nudged to the Japanese 55-year reanalysis or JRA55 (Kobayashi et al. 2015), is well validated for large-scale interhemispheric transport using sulphur hexafluoride (SF₆) and the Brewer-Dobson circulation patterns using the age of air derived from CO₂ and SF₆ (Patra et al., 2018). Thus we expect better simulations of XCO₂ by accounting for the accurate meridional and vertical profiles of CO₂. However, the convective (weekly or shorter time scale) transport remained invalidated due to the lack of appropriate observational parameters, e.g., Radon-222 with radioactive decay lifetime of 3.8 days (Patra et al., 2018).

We use monthly-mean CO₂ fluxes from JAMSTEC’s time-dependent inversion model for this analysis (Saeki and Patra 2017). The inverse model estimated CO₂ fluxes (referred to as MIROC4_Inv) for 84 regions of the globe using the MIROC4-ACTM simulations and in situ CO₂ observations at 30 sites around the globe (Figure 1). The data are provided by the National Oceanic and Atmospheric Administration (NOAA) Cooperative Air Sampling Network (Dlugokencky and Tans 2019), and Japan Meteorological Agency (JMA) (Tsuboi et al. 2013). A priori MIROC4-ACTM simulations are conducted using interannually varying emissions due to fossil-fuel and cement production (FFC) from the global carbon project (Friedlingstein et al. 2019), climatological monthly-mean terrestrial and oceanic fluxes from the Carnegie-Ames-Stanford Approach (CASA) land model and upscaling model of air-sea CO₂ flux measurements, respectively (Randerson et al., 1997; Takahashi et al., 2009). Thus, the interannual variabilities in the land and ocean regional fluxes estimated by the inverse model are driven entirely by the signals in observed CO₂ variabilities at 30 sites.

Preparation of model XCO₂ data and processing of the gridded maps and time series

Here, in order to simultaneously evaluate both the XCO₂ and CO₂ fluxes simulated by MIROC-ES2L, we first made two types of MIROC4-ACTM simulations – one is driven by the CO₂ fluxes of MIROC-ES2L and the other is by MIROC4_Inv flux; the simulations are referred to as ACTM_ES2LF and ACTM_InvF, respectively. Thus, the atmospheric CO₂ transport, driven by JRA55 reanalysis, are common for both the simulations. This experimental setting allows us to make direct comparison of XCO₂ in both simulations with that of satellite monitoring. The model simulations by MIROC4-ACTM are archived at hourly time resolution and sampled for the GOSAT and OCO-2 measurement locations by linear interpolations in horizonal grid and time (Patra et al., 2017). The model simulations are then convolved with satellite a priori (CO₂^prior) and column averaging kernels (A_i) after calculating to their respective pressure levels (P_i; where i is the index for retrieval pressure layers; 20 for OCO-2 and 15 for GOSAT) from the original ACTM vertical grids (67 hybrid). Thus the ACTM simulated XCO₂ are

XCO₂^ACTM = ∑_i (CO₂^priori . dP_i) + ∑_i A_i . dP_i (∑_i CO₂^ACTM_i - ∑_i CO₂^prior_i) (1)

where, dP_i is the pressure weighting function.

Both the simulations using MIROC4-Inv and MIROC-ES2L fluxes are spin-up from 1996-2009, so that the CO₂ concentration responses to the flux changes near the Earth’s surface propagates throughout the atmosphere, as high as the model top of about 90km. This is important because the XCO₂ measurements capture the total columns and there are systematic CO₂ gradients in the stratosphere and mesosphere that are season dependent, and lags more than 6 years for the concentration increase rate in the troposphere. Both the model concentrations are adjusted for initial values so that the global mean concentrations agree with the GOSAT observations on 01 January 2010. This is a valid approximation because we do not consider any chemical production or loss of CO₂ in the models, thus the concentration increases are consistent with the flux evolution (Basu et al. 2018). The initial value adjustment helps to put all plots on an identical XCO₂ scales.

All the XCO₂ results are gridded to 2.5^o x 2.5^o latitude-longitude grid for further analysis (Patra et al., 2017). Time series analysis are conducted by further aggregating XCO₂ data for the 15 partitions of the land and 11 ocean regions as marked by the maps in Figure 1. The model data differences and agreements are quantified by comparing the growth rates and seasonal cycles between the observed and simulated XCO₂, following decomposition of the time series using a harmonic analysis (Thoning et al., 1989). We fitted 4 harmonics to each of the regionally aggregated time series for deriving a long-term trend and a fitted time series. The seasonal cycles are calculated as fitted – trend time series, and the growth rate is calculated as time derivative of the trend time series.

Leaf Area Index (LAI) and Gross Primary Productivity (GPP)

The LAI, one-sided green leaf area per unit horizontal ground surface (m² m^-2), is one of the main drivers of primary production in the ESMs. LAI defines the canopy structure and functions of the biosphere, influenced by the weather and climate of the region. Thus, the LAI and GPP together allow us to diagnose basic ecosystem functioning for carbon assimilation in MIROC-ES2L. We used LAI from the Moderate Resolution Imaging Spectroradiometer (MODIS) Collection 6 (Yan et al. 2016) and GPP from FLUXCOM, a CO₂ flux upscaling inter-comparison project (Tramontana et al. 2016). The MODIS LAI product with original 500m resolution was aggregated globally based on the same quality control with Ichii et al. (2017) and averaged over the T42 spatial resolution for comparison with MIROC-ES2L results. The FLUXCOM GPP product (Jung et al. 2020) was generated by an ensemble of estimations by multiple machine-learning algorithms with eddy-covariance CO₂ flux observation network (FLUXNET) and MODIS land products (Tramontana et al. 2016). The original 1/12 degree resolution data were converted to the T42 spatial resolution.

Figure 2 shows the time series of CO₂ fluxes for land biosphere, ocean exchange and FFC emissions. We also show the time evolution of the meridional land and ocean CO₂ fluxes as simulated by the MIROC-ES2L and MIROC4-Inv (right column). The results show global total land and ocean CO₂ fluxes are increasing with time and offset about 44±6% of the FFC emissions during the period 2009-2018, as seen from the latest Global Carbon Budget (GCB) (Friedlingstein et al. 2019). In general, the cumulative fluxes by MIROC-ES2L (-16.0, -10.1 and 46.7 PgC for land, ocean and FFC, respectively) and MIROC4-Inv (-14.4, -8.1 and 46.3 PgC for land, ocean and FFC, respectively) are in good agreement for the overlapping GOSAT observation period of 2010-2014. These fluxes are also in good agreement with the GCB’s cumulative flux estimates -13.3, -8.4 and 47.0 PgC for land (land sink – land-use source + riverine export), ocean (ocean sink – riverine export) and FFC, respectively, during 2009-2014. For this comparison, we have corrected the GCB land and ocean fluxes for riverine export (Resplandy et al. 2018), i.e., 0.78 PgC yr^-1 is added to the land sink and removed from the ocean sink for this comparison because the inversion and ESM fluxes are used in the ACTM simulations for atmospheric CO₂ without any spatial adjustment for riverine export flux. While the GCB underestimate sinks (“budget imbalance”) (Saeki and Patra 2017; Bastos et al. 2020), we find here that the MIROC-ES2L fluxes marginally overestimate the cumulative sink compared to the inversion estimated CO₂ sink. The inversion fluxes by design reproduce the observed growth rates in atmospheric CO₂. In the ACTM simulation of atmospheric CO₂, a bias of 1 ppm is produced per 2.12 PgC of flux imbalance.

The magnitude of interannual variations and trends in CO₂ fluxes are in good agreement between the 3 different estimations for the global land but are at lower agreement for the global ocean (Fig. 2a,b). Nevertheless, the land and ocean show similar increasing long-term trends in CO₂ uptake (more negative flux in the recent years), except for the anomalous period of 1996-2002 for MIROC4-Inv. Although this anomalous period is included in the ACTM simulation spin-up, the simulated CO₂ concentrations for 2009 and later will be largely unaffected. The agreements between mean fluxes from MIROC4-InvF and MIROC-ES2L at 3 broad latitude bands (Fig. 2d-f) are excellent except for the land in the SH extratropics. The SH land flux is estimated at about -0.5 PgC yr^-1 by MIROC-InvF during 2009-2014 compared to very week negative flux by MIROC-ES2L (Fig. 2f). It has to be seen whether or not such differences in fluxes are validated/invalidated by the GOSAT and OCO-2 observations. Please bear in mind that the phase of interannual variability of CO₂ fluxes by MIROC-ES2L is not expected to match the phasing of interannual climate variability of the real world (e.g., El Niño-Southern Oscillation). Thus, MIROC4-Inv and MIROC-ES2L disagree on the phases of interannual variability of CO₂ fluxes. However, the magnitude of land flux interannual variabilities for MIROC4-Inv (0.86 PgC yr^-1, 1-s standard deviation for the period 1996-2014 after detrending) and MIROC-ES2L (0.85 PgC yr^-1) are in good agreement, but the global ocean flux interannual variabilities are underestimated largely by MIROC-ES2L (0.09 PgC yr^-1) compared to that for MIROC4-Inv (0.32 PgC yr^-1).

The seasonal variation of fluxes at different latitude grid are more variable in the case of the MIROC4-Inv and MIROC-ES2L (Fig. 3). We find that the CO₂ flux seasonalities are in good match in the latitudes north of 30^oN, but cycle of outgasing and uptake in the latitude bands of 30^oS-Eq and Eq-30^oN are contrasting between the two flux models. The MIROC-ES2L underestimates CO₂ uptake in the latitude band of 55^oS-30^oS, and show no CO₂ degassing in cold season around 60^oS along the coast of Antarctica, when compared with the MIROC4-Inv fluxes. For the simulation of XCO₂ we expect to see different phasing and amplitude of seasonal cycle simulated using the inversion and ESM fluxes, particularly over the tropical and southern hemispheric regions.

Figure 4 shows examples of XCO₂ distributions as observed by GOSAT and OCO-2 for the year 2014 and 2016, respectively. Note that OCO-2 does not have full year coverage of measurements for 2014. The data density has been significantly increased in the case of OCO-2 retrievals. We also see that the model-observation differences are generally lower for OCO-2 and ACTM_InvF compared to the differences between GOSAT and MIROC4_InvF, particularly over the ocean regions. The GOSAT sun glint observations are known to have additional retrieval bias relative to those over the land surfaces, and produces greater inconsistency when compared with transport model simulations (Patra et al., 2017; Schuh et al., 2019; Yoshida et al., 2013). Both our models systematically overestimated XCO₂ concentrations over Asia around the latitude 45^oN, which could either arise from high bias in FFC CO₂ emissions over China or underestimation of sinks over the regions. For both the simulations, XCO₂ over the tropical land regions, except over India, are underestimated (negative differences) while the XCO₂ over the ocean basins are systematically overestimated (positive differences) (Fig. 4b,c). The overestimations over ocean are more prominent in the southern extratropics.

Figure 5 shows the latitude-time distributions of zonal-mean XCO₂ for the period of GOSAT and OCO-2 measurement period. Both models are compared with GOSAT for the period 2009-2014 and only ACTM_InvF results are compared with OCO-2 due to unavailability of ACTM_ES2LF simulations for the recent years. In general, the model simulations are within 2 ppm of the observed XCO₂ concentrations. The fact that the ACTM_InvF simulation better agrees with GOSAT XCO₂ suggest an overall consistency of the in situ measurements with those from the satellites. Figure 5c,e shows that the model-observation agreements have improved compared to those using earlier versions of retrievals for both GOSAT and OCO-2, especially at the high-latitude edges (Patra et al., 2017). The ACTM_InvF better simulates the time evolution because the fluxes are optimised using in situ data, while the free running fluxes in ACTM_ES2LF marginally underestimated the XCO₂ increase rate with time due to slightly stronger global total CO₂ sinks in the years 2010-2014, compared to the inversion fluxes (Fig. 2). In the latitude range around 20^oS, the seasonal bias in ACTM_ES2L simulated XCO₂ is maximum with positive values in austral autumn and negative values in the austral spring, reflecting tendencies of weaker sink to source and weaker source to sink during the two seasons, respectively, in the MIROC-ES2L fluxes compared to the MIROC4_Inv fluxes (Fig. 3).

We find that the ACTM_InvF – GOSAT shows greater differences in the periods since 2015, which may arise from insufficient accuracy of the degradation correction of the TANSO-FTS without accounting for switching of the pointing system in January 2015 (Kuze et al. 2016). The differences are greater over the water surface than the land surface (Fig. S1 and S2). The instrumental degradation correction is suspected more than the retrieval physics uncertainties because the characteristics of surface reflectance is better modelled over the water bodies than that over the land.

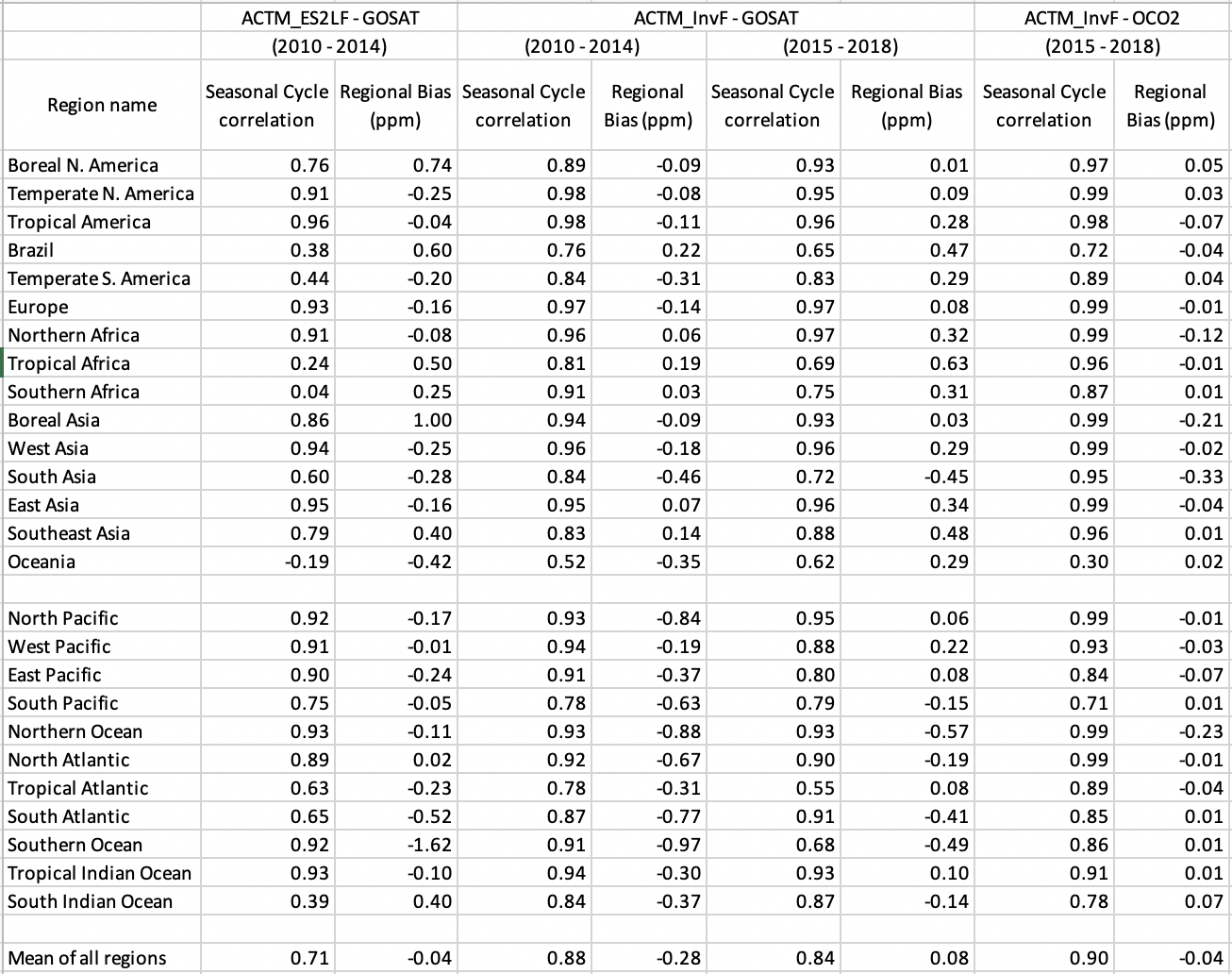
The model-observed regional biases in XCO2 (Table 1) provides an indication of how well the flux models simulated the regional fluxes. Because the GOSAT_v2.81 data are not bias corrected the agreement between ACTM_InvF with GOSAT (biases greater than 0.12 ppm for 16 out of 26 regions and are less than 1 ppm) is much greater than those for ACTM_InvF and OCO-2 (biases typically below 0.12 ppm except for 3 out of 26 regions). Generally, the regional biases are greater for ACTM_ES2LF and GOSAT_v2.81 (only 6 out of 26 regions have bias less than 0.12 ppm). The biases are systematically positive for Boreal America and Asia, in contrast to strongly negative for the Southern Ocean (poleward of 45^oS). These biases will be better assessed in the future by using newer simulations by MIROC-ES2L and updated GOSAT/GOSAT2 and OCO-2/OCO-3 retrievals.

The mean growth rates for the model and observed time series (not shown in Table 1 for clarity) suggest that the ACTM_ES2LF simulation (2.01±0.09 ppm yr^-1 for 2010-2014) slightly underestimated the GOSAT growth rates (2.13±0.25 ppm yr^-1 for 2010-2014) over all the regions. This growth rate mismatch of 0.11 ppm yr^-1 is equivalent to a sink bias of 0.25 PgC yr^-1 for MIROC-ES2L fluxes (1 ppm = 2.12 PgC in MIROC4-ACTM). As the inversion fluxes are optimised using the surface CO₂ measurements the mean growth rate from ACTM_InvF (2.32±0.04 ppm yr^-1 for 2010-2018) agrees well with that of the GOSAT (2.27±0.09 ppm yr^-1 for 2010-2018). The differences in growth rates between the regions are small because CO₂ is well mixed in the atmosphere, and also the region-to-region differences are greater over a shorter time period, e.g., for the case of GOSAT during 2010-2014, because of the impacts of regional climate variabilities on the CO₂ flux (Patra et al., 2005).

Figure 6 shows the importance of greater observational data coverage, for conducting better inversion of regional CO₂ sources and sinks, e.g., the mismatch between the seasonal cycle phase and amplitude over Southern Africa is more evident than Temperate North America. Assuming that the XCO₂ are strongly sensitive to the regional and hemispheric flux gradients we find the ACTM_ES2LF simulation shows large mismatches in the seasonal cycle phase and amplitudes in the tropical southern hemisphere to the southern extratropics (Table 1; Animation S1 and S2 for GOSAT and OCO-2, respectively). The seasonal cycle correlations are found to be smallest over Southern Africa (r=0.04), Tropical Africa (r=0.24) and Brazil (0.38). This suggests that the MIROC-ES2L fluxes are not simulated well over the tropical land regions and southern hemisphere in general (seen as the contrast between the MIROC4-Inv and MIROC-ES2L CO₂ fluxes in Fig. 3). Since the transport is common in both the ACTM simulations, we attribute the ACTM_ES2LF – GOSAT mismatches to the surface fluxes rather than the model transport uncertainty, due to the deep cumulus convection in the tropics (Remaud et al. 2018).

Better seasonal cycle correlations for South Asia (r=0.60) or Southeast Asia (r=0.79) could arise due to the far-field influence from the northern extratropics, where the fluxes are better modelled. It is typical that the terrestrial biosphere models are better parameterised for biogeochemical cycles of the temperate regions (temperature/radiation controlled), compared to the regions over tropical regions, where the carbon cycle is very strongly limited by water availability under the weaker seasonal temperature variations (Gloor et al., 2012; Haverd et al., 2013; Patra et al., 2013; Sitch et al., 2015). The tropical and temperate regions also have different characteristic of nitrogen and phosphorus limitations (Zaehle et al. 2010; Fleischer et al. 2019). The issue of poor seasonal cycle simulation by MIROC-ES2L is addressed later using empirically derived LAI and GPP.

Further, we checked the meridional variations of multi-year mean peak-to-trough seasonal cycle amplitudes (SCAs) for XCO₂ over the land and ocean regions separately (Figure 7). The interannal variabilities, seen as the vertical error bars, are generally smaller than 0.5 ppm in most latitudes, except over the ocean in the latitudes poleward of 40^oN which show persistently greater 1 ppm (Fig. 7d). We find distinct features for the comparisons over the land and ocean which helps us to identify the possible link between the surface CO₂ fluxes over the land and ocean on XCO₂. ACTM_InvF simulation generally compares well with GOSAT observations in the period 2010-2014 and OCO-2 observations in the period 2015-2018. The ACTM_ES2LF simulation shows better agreement with GOSAT observation over the land compared to ACTM_InvF simulation except over the tropics and northern extratropics (5^oS to 40^oN) (Fig. 7a). The ACTM_ES2LF simulation systematically underestimates SCAs by about 50% in the northern hemisphere (north of the Equator) compared to those observed by GOSAT over the ocean in all years. The ACTM_ES2LF and GOSAT XCO₂ SCA agreement over land in the latitudes poleward of 45^oN support the results for CMIP5 model (MIROC-ESM) and aircraft measurements showed reasonably good agreement, at about 11 ppm and 14 ppm, respectively (Graven et al. 2013). The aircraft data (Graven et al. 2013) observe combined effect of land and oceanic fluxes, thus the separation of land and ocean flux signals using XCO₂ SCA from large amount of data provide us additional information.

While the ACTM_InvF simulation shows systematically lower SCAs than those observed by GOSAT by 1.5-2.0 ppm at all latitudes over the land, the systematic disagreements of ACTM_InvF SCAs with those of OCO-2 are smaller by half (Fig. 7c). These disagreement in SCAs over land are outside the range of the interannual variability in the southern hemisphere (Fig. 7c). The SCA differences over the ocean is more striking between GOSAT_v2.81 and the other 3 estimations in the southern hemisphere (Fig. 7d). This suggests a difference in quality of XCO₂ retrievals by the two satellites, especially over the ocean (i.e., glint observations on water bodies). It is not clear whether the post-retrievals bias correction (ref. (O’Dell et al. 2018)) is the only reason for the improved agreement between OCO-2 and ACTM_InvF.

To explain the weaker seasonal cycle correlations (Table 1) and smaller seasonal cycle amplitudes (Fig. 7a) simulated by ACTM_ES2LF in the tropical regions of Africa, America and Asia, we compare two of the important terrestrial biosphere variables GPP and LAI from MIROC-ES2L with those from the FLUXCOM experiment and MODIS satellite (Fig. 8). In the tropics (10^oS-10^oN), comparisons of the two observed products (MODIS LAI and FLUXCOM GPP) show that the MODIS LAI exhibits less seasonality as the region consists of mostly evergreen forests, while FLUXCOM GPP shows distinct seasonality (Fig. 8a,c). The GPP is observed to be the highest in the late summer in both the hemispheres. This suggests that GPP seasonality in this region is controlled strongly by abiotic processes, such as precipitation or soil water, radiation and air temperature (Jung et al., 2017; Patra et al., 2005). MIROC-ES2L shows less seasonality in LAI, as in the case of MODIS LAI, but the simulated GPP shows much lesser agreement with the FLUXCOM GPP. This led us to conclude that the abiotic controls on CO₂ exchange by the terrestrial ecosystem, as modelled in MIROC-ES2L, requires further attention; it is suspected that less soil water seasonality in tropics is associated with this problem, which needs further clarification through the evaluation of the model in terms of both biogeochemical and hydrological processes (Eyring et al. 2016; Hoffman et al. 2017).

At around 30^oS, both MODIS LAI and FLUXCOM GPP show similar seasonality, suggesting LAI is the dominant controlling factor in the region. In MIROC-ES2L, the simulated LAI clearly shows weaker seasonality, leading to rather flat GPP throughout the year, suggesting problems in the biotic process model. In the northern midlatitudes (~40^oN), it is clear that the growing season is longer in MIROC-ES2L than the observation-based products, i.e., too early leaf onset and too late leaf shedding. This suggests a room for improving the phenology scheme in the model (Hajima et al. 2020). However, the problematic issues in the midlatitude regions are not tracked well in this study, and further sophistications in the atmospheric (XCO₂) metric are required.

We have compared the simulated total column CO₂ concentrations (XCO₂) by JAMSTEC’s ACTM, using CO₂ fluxes from an atmospheric CO₂ inversion (ACTM_InvF) and an ESM (ACTM_ES2LF), with the XCO₂ observed by GOSAT and OCO-2. Based on the analyses following major conclusions can be drawn.

(1) The forward transport model simulation of CO₂ fluxes from various methods can be tested well for all regions over the globe using the XCO₂ measurements from the satellites, with conditions that the transport model realistically represents the inter-hemispheric exchange and age of air in the stratosphere (Schuh et al. 2019; Calle et al. 2019). Note that the atmospheric CO₂ inversions lack in situ data coverage over much of the globe, and the ESMs are in their developmental phase for simulating the carbon cycle in a general circulation modelling framework.

(2) The inversion results using surface sites are consistent with the XCO₂ measurements over different parts of the globe within 1 ppm (or more often within 0.5 ppm) (Table 1). Although this method is only valid for the simulation period where abundant in-situ or satellite measurements are available (e.g., 2009-2014 in this study), this can be a powerful constraint to test the cotemporary CO₂ flux simulated by ESMs. Hajima et al. (2020) suggested the MIROC-ES2L is likely to underestimate the contemporary CO₂ concentration, and this study revealed that the contemporary CO₂ fluxes by the ESM are comparable to the fluxes estimated by state-of-the-art inverse models with a sink bias of 0.25 PgC yr^-1.

(3) We also propose a metric to evaluate carbon cycle processes by using of seasonal cycles of CO₂ – the inversion CO₂ fluxes and satellite XCO₂ suggested the ESM should be improved for seasonal amplitude and phasing of CO₂ fluxes in different latitude bands. Using the observation based leaf area index and gross primary productivity are compared with those simulated by the MIROC-ES2L, which suggest that the carbon-cycle processes in MIROC-ES2L need to be improved in the extratropical regions while it was suggested over the tropical regions the weather and soil water dynamics (and its ecological response) are inadequately simulated.

(4) A more sophisticated analysis is needed for removing the far-field effects on the XCO₂ over individual regions for accurately judging how well (or badly) the ESM or inversion CO₂ fluxes are modelled, as seen by the satellites. At the moment it is not very clear whether the model-observation mismatches we find over the Southern Africa region (Fig. 6c) are caused by what fraction due to regional flux error or arising from the wrong flux seasonality in other continents in the same latitude range or propagated model data mismatches from the regions north or south of Southern Africa.

(5) More of these questions will be answered better as the quality of the retrievals continues to improve and longer time series of remote sensing observations are gathered, while the ESMs account for more complex processes occurring in the earth’s environment due to both anthropogenic and natural causes. As demonstrated in this study, the evaluation of CO₂ fluxes over the globe will be a help to specify the region with large biases and to improve the model performance on reproducing CO₂ concentration, both of which are essential to make more realistic future climate projections.

Availability of data and material

The dataset(s) supporting the conclusions of this article is(are) available in JAMSTEC’s webdata server [https://ebcrpa.jamstec.go.jp/~prabir/data/Pubctn/XCO2model/].

The code of MIROC-ES2L and MIROC4-ACTM are not publicly archived because of the copyright policy of MIROC community. Readers are requested to contact the modelling group if they wish to validate the model configurations of MIROC-ES2L and MIROC4-ACTM.

Competing interests

The authors declare that they have no competing interest.

Funding

This work was supported by TOUGOU/SOUSEI, the “Integrated Research Program for Advancing Climate Models”/“Program for Risk Information on Climate Change”, by the Ministry of Education, Culture, Sports, Science, and Technology of Japan. The Earth Simulator and JAMSTEC Super Computing System were used for the simulations, and the administration staff provided much supports.

Authors' contributions

PKP and MKa proposed the research topic and conceived the analysis. TH, AI, NC, KI conducted the model simulations. RS, NC and PKP performed data analysis. TH, MKa, MKo, KI, DC joined the discussions. All authors contributed in preparation of the manuscript.

Acknowledgements

We thank Masayuki Takigawa and Shingo Watanabe, JAMSTEC for helping with the MIROC4-ACTM development. This work was first presented at the Earth Information Day, an event organised by the The Subsidiary Body for Scientific and Technological Advice (SBSTA) at the 25^th Conference of the Parties (COP-25) Madrid, Spain (https://unfccc.int/topics/science/events-meetings/systematic-observation/earth-information-day-2019). This article was first submitted to the SPEPS/Article Collection “Projection and impact assessment of global change” (05 Feb 2020).

GOSAT: Greenhouse Gases Observing Satellite; OCO-2: Orbiting Carbon Observatory (series 2); ESM: Earth System Model; ACTM: Atmospheric Chemistry-Transport Model

Andres RJ, Boden TA, Bréon F-M, Ciais P, Davis S, Erickson D, Gregg JS, Jacobson A, Marland G, Miller J, Oda T, Olivier JGJ, Raupach MR, Rayner P, Treanton K (2012) A synthesis of carbon dioxide emissions from fossil-fuel combustion. Biogeosciences 9:1845–1871 . https://doi.org/10.5194/bg-9-1845-2012
Arora V, Katavouta A, Williams RG, Jones C, Brovkin V, Friedlingstein P, Schwinger J, Bopp L, Boucher O, Cadule P, Chamberlain MA (2019) Carbon-concentration and carbon-climate feedbacks in CMIP6 models, and their comparison to CMIP5 models. Biogeosciences Discuss. https://doi.org/https://doi.org/10.5194/bg-2019-473
Arora VK, Katavouta A, Williams RG, Jones CD, Brovkin V, Friedlingstein P, Schwinger J, Bopp L, Boucher O, Cadule P, Chamberlain MA, Christian JR, Delire C, Fisher RA, Hajima T, Ilyina T, Joetzjer E, Kawamiya M, Koven CD, Krasting JP, Law RM, Lawrence DM, Lenton A, Lindsay K, Pongratz J, Raddatz T, Séférian R, Tachiiri K, Tjiputra JF, Wiltshire A, Wu T, Ziehn T (2020) Carbon–concentration and carbon–climate feedbacks in CMIP6 models and their comparison to CMIP5 models. Biogeosciences 17:4173–4222 . https://doi.org/10.5194/bg-17-4173-2020
Bastos A, O’Sullivan M, Ciais P, Makowski D, Sitch S, Friedlingstein P, Chevallier F, Rödenbeck C, Pongratz J, Luijkx IT, Patra PK, Peylin P, Canadell JG, Lauerwald R, Li W, Smith NE, Peters W, Goll DS, Jain AK, Kato E, Lienert S, Lombardozzi DL, Haverd V, Nabel JEMS, Poulter B, Tian H, Walker AP, Zaehle S (2020) Sources of Uncertainty in Regional and Global Terrestrial CO2 Exchange Estimates. Global Biogeochem Cycles 34: . https://doi.org/10.1029/2019GB006393
Basu S, Baker DF, Chevallier F, Patra PK, Liu J, Miller JB (2018) The impact of transport model differences on CO 2 surface flux estimates from OCO-2 retrievals of column average CO 2. Atmos Chem Phys 18:7189–7215 . https://doi.org/10.5194/acp-18-7189-2018
Calle L, Poulter B, Patra PK (2019) A segmentation algorithm for characterizing rise and fall segments in seasonal cycles: an application to XCO 2 to estimate benchmarks and assess model bias. Atmos Meas Tech 12:2611–2629 . https://doi.org/10.5194/amt-12-2611-2019
Chandra N, Hayashida S, Saeki T, Patra PK (2017) What controls the seasonal cycle of columnar methane observed by GOSAT over different regions in India? Atmos Chem Phys 17:12633–12643 . https://doi.org/10.5194/acp-17-12633-2017
Ciais P, Sabine C, Bala G, Bopp L, Brovkin V, Canadell JG, Chabra A, DeFries RS, Galloway J, Heimann M, Jones C, Quéré C Le, Myneni R, Piao S, Thornton P (2013) Carbon and Other Biogeochemical Cycles. In: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change
Collier N, Hoffman FM, Lawrence DM, Keppel‐Aleks G, Koven CD, Riley WJ, Mu M, Randerson JT (2018) The International Land Model Benchmarking (ILAMB) System: Design, Theory, and Implementation. J Adv Model Earth Syst 10:2731–2754 . https://doi.org/10.1029/2018MS001354
Crisp D, Pollock HR, Rosenberg R, Chapsky L, Lee RAM, Oyafuso FA, Frankenberg C, O’Dell CW, Bruegge CJ, Doran GB, Eldering A, Fisher BM, Fu D, Gunson MR, Mandrake L, Osterman GB, Schwandner FM, Sun K, Taylor TE, Wennberg PO, Wunch D (2017) The on-orbit performance of the Orbiting Carbon Observatory-2 (OCO-2) instrument and its radiometrically calibrated products. Atmos Meas Tech 10:59–81 . https://doi.org/10.5194/amt-10-59-2017
DeVries T, Le Quéré C, Andrews O, Berthet S, Hauck J, Ilyina T, Landschützer P, Lenton A, Lima ID, Nowicki M, Schwinger J, Séférian R (2019) Decadal trends in the ocean carbon sink. Proc Natl Acad Sci 201900371 . https://doi.org/10.1073/pnas.1900371116
Dlugokencky EJ, Tans PP (2019) Trends in atmospheric carbon dioxide. In: Natl. Ocean. Atmos. Adm. Earth Syst. Res. Lab.
Eldering A, O’Dell CW, Wennberg PO, Crisp D, Gunson MR, Viatte C, Avis C, Braverman A, Castano R, Chang A, Chapsky L, Cheng C, Connor B, Dang L, Doran G, Fisher B, Frankenberg C, Fu D, Granat R, Hobbs J, Lee RAM, Mandrake L, McDuffie J, Miller CE, Myers V, Natraj V, O’Brien D, Osterman GB, Oyafuso F, Payne VH, Pollock HR, Polonsky I, Roehl CM, Rosenberg R, Schwandner F, Smyth M, Tang V, Taylor TE, To C, Wunch D, Yoshimizu J (2017) The Orbiting Carbon Observatory-2: first 18 months of science data products. Atmos Meas Tech 10:549–563 . https://doi.org/10.5194/amt-10-549-2017
Eyring V, Bony S, Meehl GA, Senior CA, Stevens B, Stouffer RJ, Taylor KE (2016) Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci Model Dev 9:1937–1958 . https://doi.org/10.5194/gmd-9-1937-2016
Fleischer K, Rammig A, De Kauwe MG, Walker AP, Domingues TF, Fuchslueger L, Garcia S, Goll DS, Grandis A, Jiang M, Haverd V, Hofhansl F, Holm JA, Kruijt B, Leung F, Medlyn BE, Mercado LM, Norby RJ, Pak B, von Randow C, Quesada CA, Schaap KJ, Valverde-Barrantes OJ, Wang Y-P, Yang X, Zaehle S, Zhu Q, Lapola DM (2019) Amazon forest response to CO2 fertilization dependent on plant phosphorus acquisition. Nat Geosci 12:736–741 . https://doi.org/10.1038/s41561-019-0404-9
Friedlingstein P, Jones MW, O’Sullivan M, Andrew RM, Hauck J, Peters GP, Peters W, Pongratz J, Sitch S, Le Quéré C, DBakker OCE, Canadell1 JG, Ciais1 P, Jackson RB, Anthoni1 P, Barbero L, Bastos A, Bastrikov V, Becker M, Bopp L, Buitenhuis E, Chandra N, Chevallier F, Chini LP, Currie KI, Feely RA, Gehlen M, Gilfillan D, Gkritzalis T, Goll DS, Gruber N, Gutekunst S, Harris I, Haverd V, Houghton RA, Hurtt G, Ilyina T, Jain AK, Joetzjer E, Kaplan JO, Kato E, Goldewijk KK, Korsbakken JI, Landschützer P, Lauvset SK, Lefèvre N, Lenton A, Lienert S, Lombardozzi D, Marland G, McGuire PC, Melton JR, Metzl N, Munro DR, Nabel JEMS, Nakaoka SI, Neill C, Omar AM, Ono T, Peregon A, Pierrot D, Poulter B, Rehder G, Resplandy L, Robertson E, Rödenbeck C, Séférian R, Schwinger J, Smith N, Tans PP, Tian H, Tilbrook B, Tubiello FN, Van Der Werf GR, Wiltshire AJ, Zaehle S (2019) Global carbon budget 2019. Earth Syst Sci Data 11:1783–1838 . https://doi.org/10.5194/essd-11-1783-2019
Gloor M, Gatti L, Brienen R, Feldpausch TR, Phillips OL, Miller J, Ometto JP, Rocha H, Baker T, de Jong B, Houghton RA, Malhi Y, Aragão LEOC, Guyot J-L, Zhao K, Jackson R, Peylin P, Sitch S, Poulter B, Lomas M, Zaehle S, Huntingford C, Levy P, Lloyd J (2012) The carbon balance of South America: a review of the status, decadal trends and main determinants. Biogeosciences 9:5407–5430 . https://doi.org/10.5194/bg-9-5407-2012
Graven HD, Keeling RF, Piper SC, Patra PK, Stephens BB, Wofsy SC, Welp LR, Sweeney C, Tans PP, Kelley JJ, Daube BC, Kort EA, Santoni GW, Bent JD (2013) Enhanced Seasonal Exchange of CO2 by Northern Ecosystems Since 1960. Science (80- ) 341:1085–1089 . https://doi.org/10.1126/science.1239207
Hajima T, Watanabe M, Yamamoto A, Tatebe H, ....., Watanabe S, Kawamiya M (2020) Description of the MIROC-ES2L Earth system model and evaluation of its climate–biogeochemical processes and feedbacks. Geosci Model Dev Discuss. https://doi.org/https://doi.org/10.5194/gmd-2019-275
Hamazaki T, Kuze A, Kondo K (2004) Sensor system for Greenhouse Gas Observing Satellite (GOSAT). In: Strojnik M (ed). p 275
Hansis E, Davis SJ, Pongratz J (2015) Relevance of methodological choices for accounting of land use change carbon fluxes. Global Biogeochem Cycles 29:1230–1246 . https://doi.org/10.1002/2014GB004997
Haverd V, Raupach MR, Briggs PR, Davis SJ, Law RM, Meyer CP, Peters GP, Pickett-Heaps C, Sherman B (2013) The Australian terrestrial carbon budget. Biogeosciences 10:851–869 . https://doi.org/10.5194/bg-10-851-2013
Hoffman FM, Koven CD, Keppel-Aleks G, Lawrence DM, Riley WJ, Randerson JT, Ahlström A, Abramowitz G, Baldocchi DD, Best MJ, Bond-Lamberty B, De Kauwe MG, Denning AS, Desai AR, Eyring V, Fisher JB, Fisher RA, Gleckler PJ, Huang M, Hugelius G, Jain AK, Kiang NY, Kim H, Koster RD, Kumar S V., Li H, Luo Y, Mao J, McDowell NG, Mishra U, Moorcroft PR, Pau GSH, Ricciuto DM, Schaefer K, Schwalm CR, Serbin SP, Shevliakova E, Slater AG, Tang J, Williams M, Xia J, Xu C, Joseph R, Koch D (2017) 2016 International Land Model Benchmarking (ILAMB) Workshop Report
Houghton RA, Nassikas AA (2017) Global and regional fluxes of carbon from land use and land cover change 1850-2015. Global Biogeochem Cycles 31:456–472 . https://doi.org/10.1002/2016GB005546
Ito A, Oikawa T (2002) A simulation model of the carbon cycle in land ecosystems (Sim-CYCLE): a description based on dry-matter production theory and plot-scale validation. Ecol Modell 151:143–176 . https://doi.org/10.1016/S0304-3800(01)00473-2
Janssens-Maenhout G, Petrescu R, Crippa M, Peters J, Dentener F, van Aardenne J, Muntean M, Guizzardi D, Solazzo E, Bergamaschi P, Olivier J, Pagliari V, Oreggioni G, Doering U, Monni S, Schaaf E (2019) EDGAR v4.3.2 Global Atlas of the three major Greenhouse Gas Emissions for the period 1970&ndash;2012. Earth Syst Sci Data Discuss 2010:1–52 . https://doi.org/10.5194/essd-2018-164
Jones CD, Arora V, Friedlingstein P, Bopp L, Brovkin V, Dunne J, Graven H, Hoffman F, Ilyina T, John JG, Jung M, Kawamiya M, Koven C, Pongratz J, Raddatz T, Randerson JT, Zaehle S (2016) C4MIP &ndash; The Coupled Climate–Carbon Cycle Model Intercomparison Project: experimental protocol for CMIP6. Geosci Model Dev 9:2853–2880 . https://doi.org/10.5194/gmd-9-2853-2016
Jones CD, Frölicher TL, Koven C, MacDougall AH, Matthews HD, Zickfeld K, Rogelj J, Tokarska KB, Gillett NP, Ilyina T, Meinshausen M, Mengis N, Séférian R, Eby M, Burger FA (2019) The Zero Emissions Commitment Model Intercomparison Project (ZECMIP) contribution to C4MIP: quantifying committed climate changes following zero carbon emissions. Geosci Model Dev 12:4375–4385 . https://doi.org/10.5194/gmd-12-4375-2019
Jung M, Reichstein M, Schwalm CR, Huntingford C, Sitch S, Ahlström A, Arneth A, Camps-Valls G, Ciais P, Friedlingstein P, Gans F, Ichii K, Jain AK, Kato E, Papale D, Poulter B, Raduly B, Rödenbeck C, Tramontana G, Viovy N, Wang Y-P, Weber U, Zaehle S, Zeng N (2017) Compensatory water effects link yearly global land CO2 sink changes to temperature. Nature 541:516–520 . https://doi.org/10.1038/nature20780
Jung M, Schwalm C, Migliavacca M, Walther S, Camps-Valls G, Koirala S, Anthoni P, Besnard S, Bodesheim P, Carvalhais N, Chevallier F, Gans F, Goll DS, Haverd V, Köhler P, Ichii K, Jain AK, Liu J, Lombardozzi D, Nabel JEMS, Nelson JA, O’Sullivan M, Pallandt M, Papale D, Peters W, Pongratz J, Rödenbeck C, Sitch S, Tramontana G, Walker A, Weber U, Reichstein M (2020) Scaling carbon fluxes from eddy covariance sites to globe: synthesis and evaluation of the FLUXCOM approach. Biogeosciences 17:1343–1365 . https://doi.org/10.5194/bg-17-1343-2020
Keeling RF, Graven HD, Welp LR, Resplandy L, Bi J, Piper SC, Sun Y, Bollenbacher A, Meijer HAJ (2017) Atmospheric evidence for a global secular increase in carbon isotopic discrimination of land photosynthesis. Proc Natl Acad Sci 114:10361–10366 . https://doi.org/10.1073/pnas.1619240114
Kobayashi S, Ota Y, Harada Y, Ebita A, Moriya M, Onoda H, Onogi K, Kamahori H, Kobayashi C, Endo H, Miyaoka K, Takahashi K (2015) The JRA-55 Reanalysis: General Specifications and Basic Characteristics. J Meteorol Soc Japan Ser II 93:5–48 . https://doi.org/10.2151/jmsj.2015-001
Kondo M, Patra PK, Sitch S, Friedlingstein P, Poulter B, Chevallier F, Ciais P, Canadell JG, Bastos A, Lauerwald R, Calle L, Ichii K, Anthoni P, Arneth A, Haverd V, Jain AK, Kato E, Kautz M, Law RM, Lienert S, Lombardozzi D, Maki T, Nakamura T, Peylin P, Rödenbeck C, Zhuravlev R, Saeki T, Tian H, Zhu D, Ziehn T (2020) State of the science in reconciling top‐down and bottom‐up approaches for terrestrial CO 2 budget. Glob Chang Biol 26:1068–1084 . https://doi.org/10.1111/gcb.14917
Kulawik SS, Crowell S, Baker DF, Liu J, McKain K (2020) Characterization of OCO-2 and ACOS-GOSAT biases and errors for CO2 flux estimates. Atmos Meas Tech. https://doi.org/https://doi.org/10.5194/amt-2019-257
Kuze A, Suto H, Shiomi K, Kawakami S, Tanaka M, Ueda Y, Deguchi A, Yoshida J, Yamamoto Y, Kataoka F, Taylor TE, Buijs HL (2016) Update on GOSAT TANSO-FTS performance, operations, and data products after more than 6 years in space. Atmos Meas Tech 9:2445–2461 . https://doi.org/10.5194/amt-9-2445-2016
Le Quéré C, Andrew RM, Friedlingstein P, Sitch S, Hauck J, Pongratz J, Pickers PA, Korsbakken JI, Peters GP, Canadell JG, Arneth A, Arora VK, Barbero L, Bastos A, Bopp L, Chevallier F, Chini LP, Ciais P, Doney SC, Gkritzalis T, Goll DS, Harris I, Haverd V, Hoffman FM, Hoppema M, Houghton RA, Hurtt G, Ilyina T, Jain AK, Johannessen T, Jones CD, Kato E, Keeling RF, Goldewijk KK, Landschützer P, Lefèvre N, Lienert S, Liu Z, Lombardozzi D, Metzl N, Munro DR, Nabel JEMS, Nakaoka S, Neill C, Olsen A, Ono T, Patra P, Peregon A, Peters W, Peylin P, Pfeil B, Pierrot D, Poulter B, Rehder G, Resplandy L, Robertson E, Rocher M, Rödenbeck C, Schuster U, Schwinger J, Séférian R, Skjelvan I, Steinhoff T, Sutton A, Tans PP, Tian H, Tilbrook B, Tubiello FN, van der Laan-Luijkx IT, van der Werf GR, Viovy N, Walker AP, Wiltshire AJ, Wright R, Zaehle S, Zheng B (2018) Global Carbon Budget 2018. Earth Syst Sci Data 10:2141–2194 . https://doi.org/10.5194/essd-10-2141-2018
Monsi M, Saeki T (1953) Über den Lichtfaktor in den Pflanzengesellschaften und seine Bedeutung für die Stoffproduktion. Japanese J Bot 14:22–52
O’Dell CW, Eldering A, Wennberg PO, Crisp D, Gunson MR, Fisher B, Frankenberg C, Kiel M, Lindqvist H, Mandrake L, Merrelli A, Natraj V, Nelson RR, Osterman GB, Payne VH, Taylor TE, Wunch D, Drouin BJ, Oyafuso F, Chang A, McDuffie J, Smyth M, Baker DF, Basu S, Chevallier F, Crowell SMR, Feng L, Palmer PI, Dubey M, García OE, Griffith DWT, Hase F, Iraci LT, Kivi R, Morino I, Notholt J, Ohyama H, Petri C, Roehl CM, Sha MK, Strong K, Sussmann R, Te Y, Uchino O, Velazco VA (2018) Improved retrievals of carbon dioxide from Orbiting Carbon Observatory-2 with the version 8 ACOS algorithm. Atmos Meas Tech 11:6539–6576 . https://doi.org/10.5194/amt-11-6539-2018
Orr JC, Najjar RG, Aumont O, Bopp L, Bullister JL, Danabasoglu G, Doney SC, Dunne JP, Dutay J-C, Graven H, Griffies SM, John JG, Joos F, Levin I, Lindsay K, Matear RJ, McKinley GA, Mouchet A, Oschlies A, Romanou A, Schlitzer R, Tagliabue A, Tanhua T, Yool A (2017) Biogeochemical protocols and diagnostics for the CMIP6 Ocean Model Intercomparison Project (OMIP). Geosci Model Dev 10:2169–2199 . https://doi.org/10.5194/gmd-10-2169-2017
Patra P, Crisp D, Kaiser J, Wunch D, Saeki T, Ichii K, Sekiya T, Wennberg PO, Feist DG, Pollard DF, Griffith DWT, Velazco VA, De Maziere M, Sha MK, Roehl C, Chatterjee A, Ishijima K (2017) The Orbiting Carbon Observatory (OCO-2) tracks 2–3 peta-gram increase in carbon release to the atmosphere during the 2014–2016 El Niño. Sci Rep 7:13567 . https://doi.org/10.1038/s41598-017-13459-0
Patra PK, Canadell JG, Houghton RA, Piao SL, Oh N-H, Ciais P, Manjunath KR, Chhabra A, Wang T, Bhattacharya T, Bousquet P, Hartman J, Ito A, Mayorga E, Niwa Y, Raymond PA, Sarma VVSS, Lasco R (2013) The carbon budget of South Asia. Biogeosciences 10:513–527 . https://doi.org/10.5194/bg-10-513-2013
Patra PK, Ishizawa M, Maksyutov S, Nakazawa T, Inoue G (2005) Role of biomass burning and climate anomalies for land-atmosphere carbon fluxes based on inverse modeling of atmospheric CO 2. Global Biogeochem Cycles 19: . https://doi.org/10.1029/2004GB002258
Patra PK, Niwa Y, Schuck TJ, Brenninkmeijer CAM, Machida T, Matsueda H, Sawa Y (2011) Carbon balance of South Asia constrained by passenger aircraft CO2 measurements. Atmos Chem Phys 11:4163–4175 . https://doi.org/10.5194/acp-11-4163-2011
Patra PK, Takigawa M, Watanabe S, Chandra N, Ishijima K, Yamashita Y (2018) Improved Chemical Tracer Simulation by MIROC4.0-based Atmospheric Chemistry-Transport Model (MIROC4-ACTM). SOLA 14:91–96 . https://doi.org/10.2151/sola.2018-016
Randerson JT, Thompson M V., Conway TJ, Fung IY, Field CB (1997) The contribution of terrestrial sources and sinks to trends in the seasonal cycle of atmospheric carbon dioxide. Global Biogeochem Cycles 11:535–560 . https://doi.org/10.1029/97GB02268
Remaud M, Chevallier F, Cozic A, Lin X, Bousquet P (2018) On the impact of recent developments of the LMDz atmospheric general circulation model on the simulation of CO&lt;sub&gt;2&lt;/sub&gt; transport. Geosci Model Dev 11:4489–4513 . https://doi.org/10.5194/gmd-11-4489-2018
Resplandy L, Keeling RF, Rödenbeck C, Stephens BB, Khatiwala S, Rodgers KB, Long MC, Bopp L, Tans PP (2018) Revision of global carbon fluxes based on a reassessment of oceanic and riverine carbon transport. Nat Geosci 11:504–509 . https://doi.org/10.1038/s41561-018-0151-3
Saeki T, Patra PK (2017) Implications of overestimated anthropogenic CO2 emissions on East Asian and global land CO2 flux inversion. Geosci Lett 4:9 . https://doi.org/10.1186/s40562-017-0074-7
Schuh AE, Jacobson AR, Basu S, Weir B, Baker D, Bowman K, Chevallier F, Crowell S, Davis KJ, Deng F, Denning S, Feng L, Jones D, Liu J, Palmer PI (2019) Quantifying the Impact of Atmospheric Transport Uncertainty on CO 2 Surface Flux Estimates. Global Biogeochem Cycles 33:484–500 . https://doi.org/10.1029/2018GB006086
Sitch S, Friedlingstein P, Gruber N, Jones SD, Murray-Tortarolo G, Ahlström A, Doney SC, Graven H, Heinze C, Huntingford C, Levis S, Levy PE, Lomas M, Poulter B, Viovy N, Zaehle S, Zeng N, Arneth A, Bonan G, Bopp L, Canadell JG, Chevallier F, Ciais P, Ellis R, Gloor M, Peylin P, Piao SL, Le Quéré C, Smith B, Zhu Z, Myneni R (2015) Recent trends and drivers of regional sources and sinks of carbon dioxide. Biogeosciences 12:653–679 . https://doi.org/10.5194/bg-12-653-2015
Takahashi T, Sutherland SC, Wanninkhof R, Sweeney C, Feely RA, Chipman DW, Hales B, Friederich G, Chavez F, Sabine C, Watson A, Bakker DCE, Schuster U, Metzl N, Yoshikawa-Inoue H, Ishii M, Midorikawa T, Nojiri Y, Körtzinger A, Steinhoff T, Hoppema M, Olafsson J, Arnarson TS, Tilbrook B, Johannessen T, Olsen A, Bellerby R, Wong CS, Delille B, Bates NR, de Baar HJW (2009) Climatological mean and decadal change in surface ocean pCO2, and net sea–air CO2 flux over the global oceans. Deep Sea Res Part II Top Stud Oceanogr 56:554–577 . https://doi.org/10.1016/j.dsr2.2008.12.009
Tans PP, Keeling RF (2019) Trends in Atmospheric Carbon Dioxide. NOAA/ESRL Scripps Inst Oceanogr
Thoning KW, Tans PP, Komhyr WD (1989) Atmospheric carbon dioxide at Mauna Loa Observatory: 2. Analysis of the NOAA GMCC data, 1974-1985. J Geophys Res Atmos 94:8549–8565 . https://doi.org/10.1029/JD094iD06p08549
Tramontana G, Jung M, Schwalm CR, Ichii K, Camps-Valls G, Ráduly B, Reichstein M, Arain MA, Cescatti A, Kiely G, Merbold L, Serrano-Ortiz P, Sickert S, Wolf S, Papale D (2016) Predicting carbon dioxide and energy fluxes across global FLUXNET sites with regression algorithms. Biogeosciences 13:4291–4313 . https://doi.org/10.5194/bg-13-4291-2016
Tsuboi K, Matsueda H, Sawa Y, Niwa Y, Nakamura M, Kuboike D, Saito K, Ohmori H, Iwatsubo S, Nishi H, Hanamiya Y, Tsuji K, Baba Y (2013) Evaluation of a new JMA aircraft flask sampling system and laboratory trace gas analysis system. Atmos Meas Tech 6:1257–1270 . https://doi.org/10.5194/amt-6-1257-2013
Watanabe S, Hajima T, Sudo K, Nagashima T, Takemura T, Okajima H, Nozawa T, Kawase H, Abe M, Yokohata T, Ise T, Sato H, Kato E, Takata K, Emori S, Kawamiya M (2011) MIROC-ESM 2010: Model description and basic results of CMIP5-20c3m experiments. Geosci Model Dev 4:845–872 . https://doi.org/10.5194/gmd-4-845-2011
Wunch D, Wennberg PO, Osterman G, Fisher B, Naylor B, Roehl CM, O&apos;Dell C, Mandrake L, Viatte C, Kiel M, Griffith DWT, Deutscher NM, Velazco VA, Notholt J, Warneke T, Petri C, De Maziere M, Sha MK, Sussmann R, Rettinger M, Pollard D, Robinson J, Morino I, Uchino O, Hase F, Blumenstock T, Feist DG, Arnold SG, Strong K, Mendonca J, Kivi R, Heikkinen P, Iraci L, Podolske J, Hillyard PW, Kawakami S, Dubey MK, Parker HA, Sepulveda E, García OE, Te Y, Jeseck P, Gunson MR, Crisp D, Eldering A (2017) Comparisons of the Orbiting Carbon Observatory-2 (OCO-2) X CO 2 measurements with TCCON. Atmos Meas Tech 10:2209–2238 . https://doi.org/10.5194/amt-10-2209-2017
Yan K, Park T, Yan G, Chen C, Yang B, Liu Z, Nemani R, Knyazikhin Y, Myneni R (2016) Evaluation of MODIS LAI/FPAR Product Collection 6. Part 1: Consistency and Improvements. Remote Sens 8:359 . https://doi.org/10.3390/rs8050359
Yokota T, Yoshida Y, Eguchi N, Ota Y, Tanaka T, Watanabe H, Maksyutov S (2009) Global Concentrations of CO2 and CH4 Retrieved from GOSAT: First Preliminary Results. SOLA 5:160–163 . https://doi.org/10.2151/sola.2009-041
Yoshida Y, Kikuchi N, Morino I, Uchino O, Oshchepkov S, Bril A, Saeki T, Schutgens N, Toon GC, Wunch D, Roehl CM, Wennberg PO, Griffith DWT, Deutscher NM, Warneke T, Notholt J, Robinson J, Sherlock V, Connor B, Rettinger M, Sussmann R, Ahonen P, Heikkinen P, Kyrö E, Mendonca J, Strong K, Hase F, Dohe S, Yokota T (2013) Improvement of the retrieval algorithm for GOSAT SWIR XCO 2 and XCH 4 and their validation using TCCON data. Atmos Meas Tech 6:1533–1547 . https://doi.org/10.5194/amt-6-1533-2013
Zaehle S, Friend AD, Friedlingstein P, Dentener F, Peylin P, Schulz M (2010) Carbon and nitrogen cycle dynamics in the O-CN land surface model: 2. Role of the nitrogen cycle in the historical terrestrial carbon balance. Global Biogeochem Cycles 24:n/a-n/a . https://doi.org/10.1029/2009GB003522

Table 1. Statistics of XCO₂ time series simulations in comparison with GOSAT and OCO-2 measurements. Correlations coefficients are calculated for the mean seasonal cycles of the time series as calculated by harmonic analysis. Mean XCO₂ biases are calculated as the differences for the overlapping periods between two data records. The regions are arranged from North to South latitudes within each of the continents and ocean basins, as much as possible.

Download PDF

Journal Publication

published 14 Apr, 2021

Read the published version in Progress in Earth and Planetary Science →

Editorial decision: Major revision
14 Nov, 2020
Review #1 received at journal
11 Nov, 2020
Review #2 received at journal
18 Oct, 2020
Reviewer #2 agreed at journal
15 Oct, 2020
Reviewers invited by journal
14 Oct, 2020
Reviewer #1 agreed at journal
14 Oct, 2020
Editor assigned by journal
06 Oct, 2020
Submission checks completed at journal
05 Oct, 2020
Editor invited by journal
05 Oct, 2020

You are reading this older preprint version

Read the latest preprint version →

Evaluation of Earth System Model and Atmospheric Inversion using Total Column CO₂ Observations from GOSAT and OCO-2

Status:

Journal Publication

Version 2

Abstract

Figures

Introduction

Methods

Results And Discussion

Conclusions

Declarations

Abbreviations

References

Tables

Supplementary Files

Status:

Journal Publication

Version 2